大家好,今天继续为大家分享初中数学知识!我们知道,我们所做的题目,尤其是几何证明题,好多都是有一些基本的图形通过旋转变换,拉伸而出来的图形,然后把已知条件再做改变就出来一道新的题目。今天就给大家分享一下我们几何题目中常见的十种基本图形,我们把这些基本图形认识清楚了,我们再开始进行慢慢变换,给它们“整下容,穿穿衣服”看看你们还认识不。
基本图形(1)

这是最常见的直线形状,很简单了,但是有两个重要的规律要记住,若AC=BD则AB=CD,当然相反也是成立的。
基本图形(2)
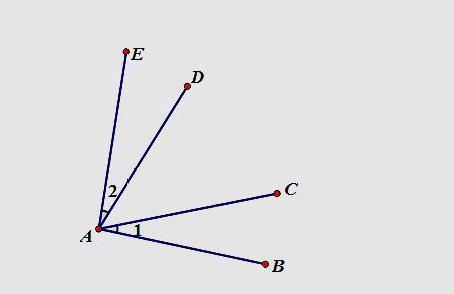
上面一个是线段的最基本的图形,这个是角最基础的图形,这里的规律就是若∠1=∠2,则∠EAC=∠DAB,当然它的逆命题也是成立的。
基本图形(3)——箭头模型

这个图形我们在做题时候见得就比较多了,记住一个规律∠1 ∠2=∠3 ∠4 ∠B ∠C,也就是∠BPC=∠A ∠B ∠C。我们在做题过程中,发现这个形状就能找到这个规律,在我们求角的度数,证明三角形全等等好多情况下都能用到。
基本图形(4)——蝶形

这个形状相信都不陌生,都见过它的好多变种,但无论怎么变有一个规律是不会变的,那就是∠A ∠B=∠C ∠D。
基本图形(5)

如上图,A、O、B在同一直线上,OD、OE分别平分∠AOC和∠BOC,则有OD⊥OE,或∠DOE=90°。
基本图形(6)

上图模型是不是有点熟悉,前面的箭头模型多穿了点衣服,但是如果这个模型还满足BP、CP是角平分线的话,咋还有∠BPC=90° 1/2∠BAC
基本图形(7)

如上图,①AC平分∠DAB,②AD=CD,③DC∥AB,这个模型如果满足前面三个条件中的任两个,那么就能推出第三个。
基本图形(8)

这个是角平分线定理和逆定理的模型不再说了,就是AP为角平分线,则PC=PB,反过来也成立!
基本图形(9)

这个图形已经复杂了,严格地说已经不能算基本图形,但在实际应用中比较常见还是单列,它是蝶形,箭头形状组合而成。如果ab,CDE在同一直线上,那么夹在两平行线间同底的三角形面积相等,或者等底等高的三角形面积相等。
基本图形(10)

这个也是复杂图形,“洋葱形”。CH垂直平分AB,则CA=CB,DA=DB,EA=EB,FA=FB,GA=GB,HA=HB。同样反过来也是成立的。有些朋友可能已经看出来了,这是垂直平分线的定理与逆定理。
以上就是几何中常见的十种基本图形,我们把这些结论掌握了,以后做题基本能够得心应手,不会再手足无措了。
今天就给大家分享到这里,如果喜欢那么就关注转发点赞,有别的想法可以在评论区留言,谢谢
,




