将一元函数积分推广来看对于连续函数 f(x,y) 如何求二重积分. 每个二重积分都可以方便地用定积分的方法分步进行计算.
矩形区域上的二重积分设 f(x,y) 在矩形区域 R: a<=x<=b, c<=y<=d 上有定义. 如果 R 被分别平行于 x 轴和 y 轴的直线网格所划分成许多小块面积 ∆ A="∆ x∆ y" . 如下动画所示

当网格不断进行细分使 ∆x 和 ∆y 都趋近零时, 则趋于 R 的面积趋近于极限值, 则称该极限值为 f 在 R 上的二重积分, 记为:

值得注意的是 f 函数的连续性是二重积分存在的一个充分条件, 对于许多不连续的函数, 该极限也存在.
二重积分的性质连续函数的二重积分也有一些代数性质:

当 f(x,y) 为正函数时, 则可以把矩形区域 R 上的 f 函数二重积积分视为曲面为 z=f(x,y) 的棱柱体的体积.

现在 计算 xy 平面内矩形区域 R : 0<=x<=2, 0<=y<=1 在平面 z=4-x-y 下面的体积。 求其二重积分的过程请看下面的动画。
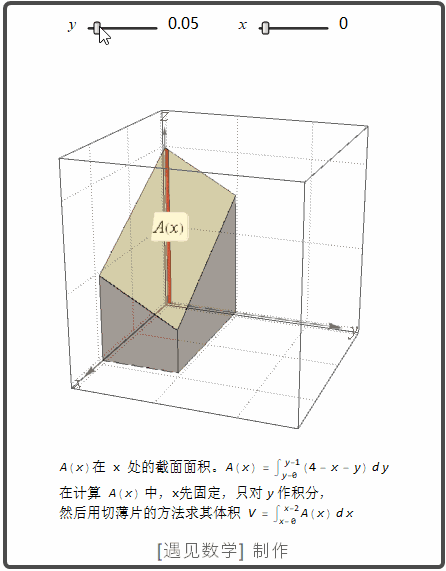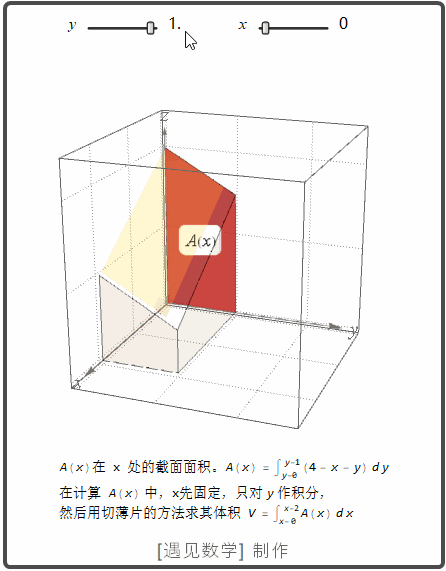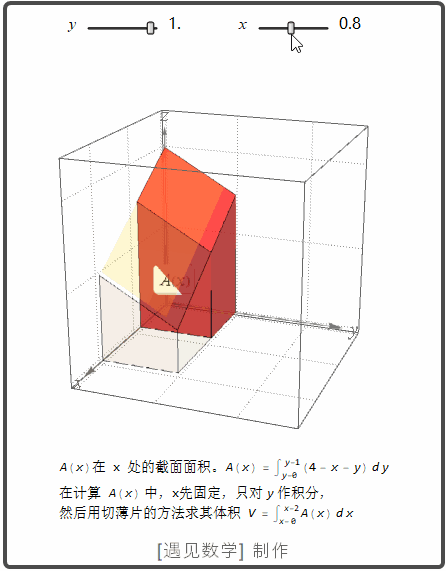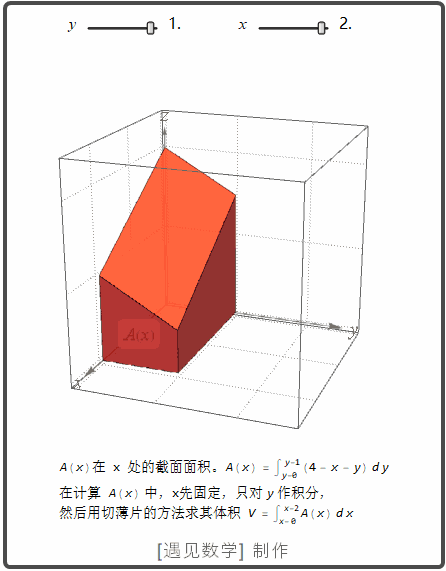
也就是说体积可以这样计算出来: 先固定 x, 将 4-xy 先关于 y 从 y=0 到 y=1, 然后再对所得 x 的表达式关于 x 从 x=0 到 x=2 积分. 则体积可以写成表达式:

上述表达式称为二重积分或累次积分(iterated integral).
Guido Fubini(圭多.富比尼) 在1907年证明了矩形域上任意一个连续函数的二重积分都可以用两种累次积分的任一种次序计算.


函数 f(x,y) 在非矩形区域 R 上的二重积分, 设想被网格覆盖, 不过在 R 内的小块面积为红色, 如下图所示:

可以看到随着网格不断细分, R内包含的小矩形方块越来越趋于零时, S 就会有极限, 则称该极限为 f 在 R 上的二重积分:

如果 f(x,y) 为正, 且在 R 上连续, 则曲面 z=ff(x,y) 与 R 之间的立体趋于的体积为:

观看下面的动画:

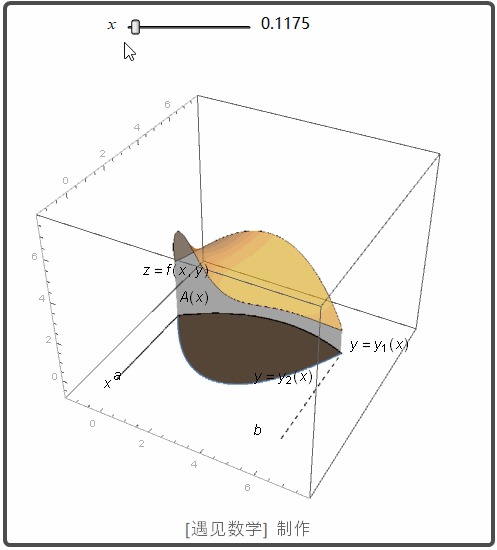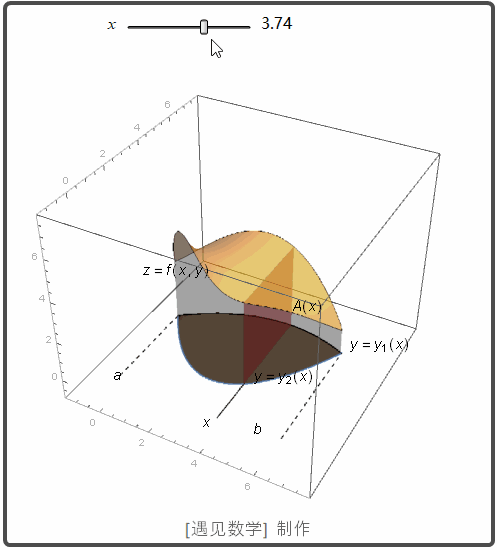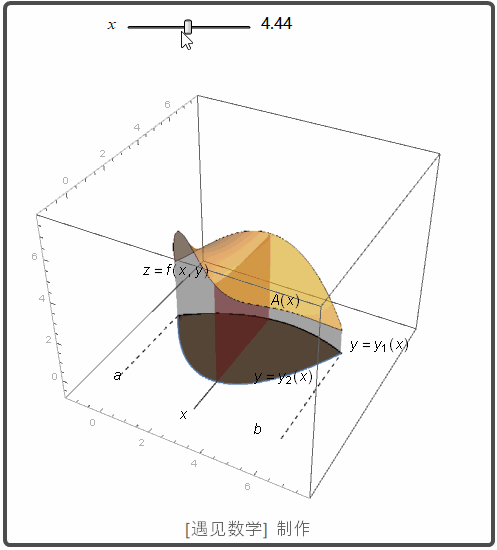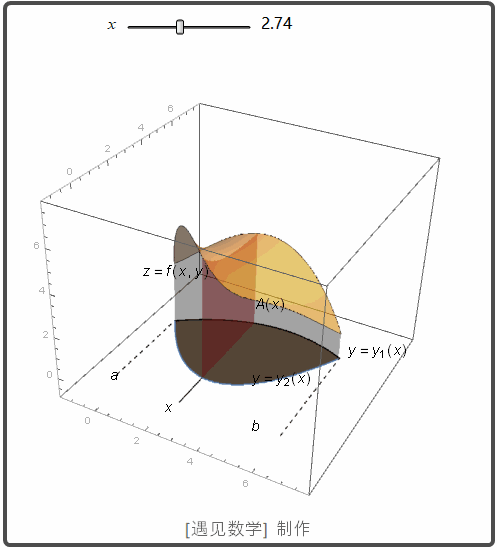
在 xy 平面内, 如果 R 是一个由两条曲线 g1(x) 和 g2(x) 围城的区域. 则也可以用切片法来求体积. 先计算截面面积 A(x):

然后再对 A(x) 从 x=a 到 x=b 作积分可以求得体积:

观察下面动画 A(x) 从 x=a 到 x=b 作积分的过程: