中线最值问题（谈谈最值问题中的等周问题）

前言

等周问题,就是要在周长条件等同的所有区域中,找出面积最大的区域.所以等周问题属于极值问题范畴.

等周问题是一个古老的问题,同时又是一个有着广泛应用的,并在不断发展的问题.

学习方法是多种多样的,可以先看本书后记,在了解了本书的主要精神之后,再从头来认真阅读正文,领会“对称性”和“反射法”.

后记

北京市1978年中学生数学竞赛第二试的最后一题是这样的:“设有一直角QOP,试在 OP边上求一点A,在OQ边上求一点B,在直角内求一点C,使BC CA等于定长L,且使四边形ACBO的面积最大.”2000多名优秀选手中的绝大部分没有做出来,只有胡波一人答对了。它可能是这次竞赛最难的一题.听过“等周问题”演讲的一些同学也没有做出来，说明目前中学生的学习方法与学习深度还有一些问题.为便于中学生学习,将这小册子的主要精神介绍一下.

中线最值问题（谈谈最值问题中的等周问题）(1)

封面图

念完全书,在结论上，即定理内容上应该有这么一个印象:达到极值的几何图形往往都具有对称性.比如:内接同一圆周的所有n边形中,正n边形的面积最大;周长为给定值的一切n边形中,正n边形的面积最大;周长一定的所有封闭平面曲线中,圆周所围的面积最大.正n边形是对称性很强的几何图形.至于圆周那是对称性最强的几何图形.通过圆心的任何直线都是它的对称轴,圆心是它的对称中心.深思一下可以发现:“达到极值的几何图形往往都具有对称性”在第2节的引理2和引理3中就已显示出来.

根据第2节的引理2和引理3,上述竞赛试题是容易直接求解的(请对照《北京科技报》(1978年)第五期或《北京日报》1978年5月8日的竞赛题解).

念完全书,在方法上即解题技巧上应该有这么一个印象:这本册子一直在使用反射法——求作关于直线或平面的对称点或对称图形的方法.在第2节引理3的简单证明中“作B关于直线l的对称点B'”,在第5节定理2的证明中,特别在圆和球的极值性质这两节中,都使用着反射法.这种反射法在求解某些几何问题和其他极值问题时，也很有用处.在物理的光学和电磁学里也很有用处,物理学家们称它为镜像法.

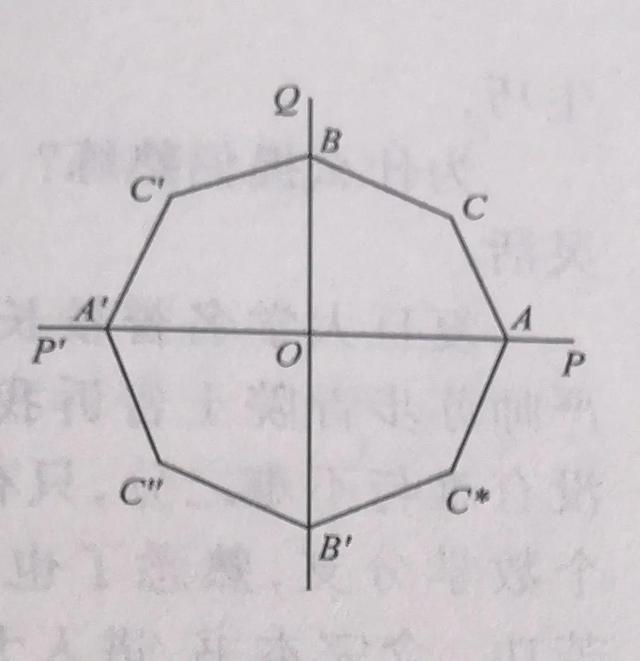
如果读者熟悉反射法且记得“周长给定的 n 边形中,正n边形的面积最大”,上述竞赛试题一下子就解决了.因为将直角QOP以OQ为对称轴反射过去成为QOP'，再将图形以P'P为对称轴反射下来,四边形ACBO就反射成八边形ACBC'A'C"B'C﹡(见下页图).周长给定为4L的八边形中，以边长为L/2的正八边形的面积最大.正八边形在第一象限的三个顶点 A、C、B就是所求的解.

中线最值问题（谈谈最值问题中的等周问题）(2)

话得说回来，1965年冬有过这么回事:某公社要铺设小水渠，每段用三块同样宽度l的长方形水泥板拼成水槽。一块在底面,两块在水渠的侧面.当侧面两块水泥板都和底面垂直时,水渠横截面的面积为l².当侧边两块水泥板张开时,横截面的面积将增大,到一定程度后将减少.当两个内角都张到180°时,横截面的面积为零.横截面面积直接反映水渠水容量的大小,公社急需知道,内角多少度时,横截面面积达到最大.一位社教工作队的同志返回原单位,用微积分的办法，选取两个内角θ与φ作为参数,花了两个晚上证明出当两个内角都是120°时,水容量最大.其实,只要将横截面按开口线反射一下,就成为周长给定的六边形，什么时候面积最大?正六边形.或者边长给定的六边形什么时候面积最大?内接于圆.最后结论都是内角等于120°.这位同志是有水平、有能力的,问题是他对“等周”不熟,关键在于要熟,要熟练,俗语说:熟能生巧.

为什么提倡熟练?因为熟练包含了牢固与灵活.

复旦大学名誉校长、我学习黎曼几何时的严师苏步青院士告诉我,数学对某一个人来说没有难与不难之分,只有熟与不熟之分,深入这个数学分支，熟悉了也就不难了.要熟就要下苦功.念完本书，进入大学后，可念念苏老的专著《微分几何五讲》，该书第一讲的第一节就是讲述“等周问题”.那里是用高等数学方法证明的.

蔡宗熹

2001年劳动节于北京学院路31号原地矿部计算中心

中线最值问题（谈谈最值问题中的等周问题）(3)