不用再为解一般的一元四次方程烦恼了,因为老黄已经帮你找到了一般的方法——配方法,最后还推出了解一元四方程的公式。过程复杂,多余的话就不说了,直入主题:

用老黄这个方法解一般的一元四次方程 :x^4 bx^3 cx^2 dx e=0,要先把它化成x^4 cx^2 dx e=0,就是三次项系数等于0的形式,或称为缺失三次项的形式。
具体的转化方法是运用换元法,记x=t-α (α是常数),只要我们能求得t,自然也就能求得x。然后把x=t-α代入原方程,可以得到:
(t-α)^4 b(t-α)^3 c(t-α)^2 d(t-α) e=0,将这个关于t的四次方程展开,三次项的系数是4α b, 只要α=-b/4,那么这个关于t的四次方程的三次项系数就等于0,从而得到一个缺失三次项的关于t的四次方程。
现在我们只要解x^4 cx^2 dx e=0这个形式的四次方程,就可以实现解任意一元四次方程了。下面我们称它为“可解形式”。
四次方程有四个根,记为x1, x2, x3, x4,其中任意两个根,都可以看作是一个二次方程的根,剩下两个根又是另一个二次方程的根。因此,任意四次方程都可以化作关于x的方程:(x^2 px q)(x^2 sx t)=0的形式。我们设二次多项式A和一次多项式B,使A B=x^2 px q,A-B=x^2 sx t,就可以求得多项式A和B。因此任意四次方程又可以化为A^2-B^2=0的形式。
对可解形式来说,由于三次项的系数为0,因此A必为x^2 h的形式, B必为r(x k)的形式。其中h, k, r都是常数。否则就一定会出现三次项的系数不为0的情况,产生矛盾。从而,我们可以将任意可解形式配方成(x^2 h)^2-r(x k)^2=0的形式。
将配方的形式展开,得x^4 (2h-r)x^2-2rkx h^2-rk^2=0. 因此得到关于h,k,r的三元方程组:
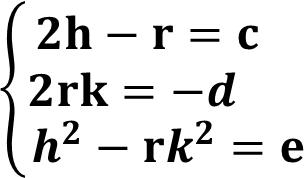
转化方程组可以得到一个关于r的三次方程,r^3 2cr^2 (c^2-4e)r-d^2=0. 而三次方程是有现成的公式可以运用的。这里会有三个r值。它们分别对应着,确定x^2 px q=0的一个根,如x1后,另一个根是x2, x3, 或x4三种情况。换句话说,我们取任意一个r值,最后都能得到原方程的四个根。所以我们就取最简单的那个:

并且根据h=(c r)/2,k=-d/(2r),求得h, k的值.
再由配方式运用平方差公式,得到(x^2 x根号r h k根号r)(x2-x根号r h-k根号r)=0. 并解得:

这就完成了任意一元四次方程的求解过程,并且得到了其求根的公式。 其公式归纳如下图:

最后,我们举一个例子,来检验这个解法。为了减少运算量,这里选择直接举一个缺失三次项的一元四次方程:x^4-2x^2 8x-3=0.
其中c=-2, d=8, e=-3. 因此p=32/3, q=-1280/27.

h=(c r)/2=1, k=-d/(2r)=-1,
因此原方程的根为:x1=-1 根号2, x2=-1-根号2, x3=1 i根号2, x4=1-i根号2.
经检验,这四个根都是原方程的解。可见老黄这个解法是正确的。
,




