撰文 | 夏志宏(南方科技大学讲座教授、数学系主任,美国西北大学终身教授)
现代科学是从牛顿开始的,他是一位非常了不起的科学家。众所周知,他发现了万有引力定律还有牛顿力学,还是微积分发现人之一。从一个人对科学的贡献来讲,很少有人可以与牛顿相提并论,一生能如果做上述一件事,就能被称为非常伟大的科学家了,牛顿却做了三件。

关于牛顿,有一个家喻户晓的传说:牛顿在睡午觉的时候,一个苹果掉在他的头上,由此激发了他的灵感,从而发现了万有引力定律,这也是整个现代科学的起源。我的母校南京大学曾得到英国剑桥大学里这颗苹果树的种子,大家如果想看到这棵砸过牛顿的苹果树的后代,可以到南京大学的新校园。

这幅漫画上有一段很有意思的笑话,大意是:我想下面更难的事,是怎么申请科研经费,总不能因为苹果掉在我头上就可以得到资助了。
或许大家觉得牛顿发现万有引力是个偶然的幸运,但事实上并非如此,万有引力定律的发现经历了前人很多年的观测。
类似的例子还有开普勒发现行星运动三大定律,(编者注:椭圆定律:所有行星绕太阳的轨道都是椭圆,太阳在椭圆的一个焦点上;面积定律:行星和太阳的连线在相等的时间间隔内扫过相等的面积;调和定律:所有行星绕太阳一周的恒星时间的平方与它们轨道长半轴的立方成比例。)开普勒三大定律的发现同样也不是偶然,不是灵机一现。

历史上第一个被尿憋死的科学家:第谷·布拉赫
开普勒发现了行星运动三大定律之前,有一位丹麦的数学家第谷·布拉赫,他花了很多时间去观察行星的运动,那时观测精度比较差,他又是用肉眼来观察行星的运动,因此花费了很多精力。

丹麦皇帝甚至资助他在岛上修建天文台,花了很多钱来支持他的研究,有意思的是,当时他记录的纸都是一个专门的造纸厂提供的。
第谷和皇帝关系很好,但是皇帝死后,继任皇帝不喜欢他,他就跑到布拉格去,那里的皇帝也非常支持他进行科学研究,第谷得以经常出没皇宫。有一次他在皇宫喝了很多酒,回家后就死掉了,大家一直猜测他是什么原因死亡,有一种猜测是被别人下毒,另一种猜测是喝多了被尿憋死。
在他死后的四百多年,也就是2001年,有人决定把他的尸体挖出来,来确定他的死因,结果发现果然不是毒死的,而是被尿憋死的,第谷成了历史上第一个被尿憋死的科学家。
又过了十年,关于第谷又有一个很大的争议。第谷性格怪异,在二十几岁的时候跟堂兄争吵谁是更伟大的数学家,最后两人决定决斗,结果第谷的鼻子在决斗中被割掉,大家很长时间不知道他的鼻子是金子做的还是银子做的。2010年,大家决定再把他的棺材挖出来研究一下,结果发现他的鼻子是铜做的。
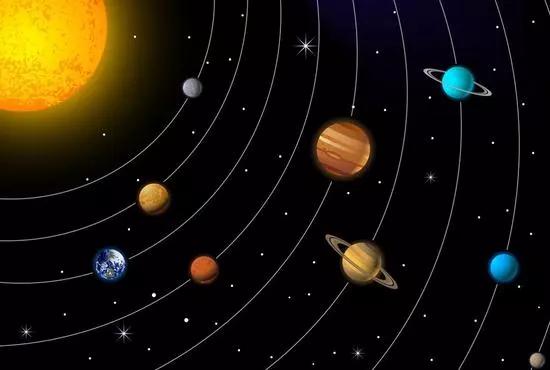
第谷对天文学的观测奠定了开普勒的基础、奠定了万有引力定律的开始。作为他的学生,开普勒观测了火星运动。如果当初没有观测火星的话,大家会认为行星的轨道是圆形的,所以牛顿才终于发现了万有引力,而并不仅仅是因为一个苹果掉在他的头上。
用经典方法无法解决三体问题
当牛顿发现万有引力定律后,第一个问题是想解决多体问题,既有万有引力,又有牛顿力学,再加上微积分,这样的天文学问题变成了数学问题。

如何根据这些物理定律来找到行星运动的轨道,精确地推算轨道。太阳和一个行星在一起就是二体问题,我们已经知道二体问题的轨道是稳定性轨道,而太阳与两个行星放在一起就叫三体问题,天体越多就变成越复杂的数学问题。三体问题花了很长时间,最终人们发现三体问题是不可解的。
太阳系远远超过三体,有太阳,有行星,行星还有卫星,还有其他很多小天体。整个太阳系是一个庞大的体系,远远超过三体,是更复杂的多体问题。既然三体问题都没法解,对于多体问题,用经典的方法去解决太阳系的运动,显然也是不太可能的。
这里需要再提一下牛顿,他同样也是位“怪”人,上半辈子做了非常伟大的科学工作,但他是非常虔诚的基督徒,认为太阳系是不稳定的。人们会问太阳系既然不稳定,那人类怎么可能生存?牛顿的解释是,上帝每隔一段时间就来推一下行星或者球,让地球回到稳定的轨道上不会偏离太远。
牛顿一直试图用数学的方法来证明上帝的存在,用数学公式去解开行星的轨道,现在看来非常荒唐的,所以有人开玩笑的说,牛顿被苹果砸了后,大脑其实不太好了。
关于行星的稳定性,每一位伟大的科学家都会提出自己的见解,这些见解有时候介于数学分析,有时候介于猜测。

《三体》小说为什么非常有趣?
大家都知道数学家喜欢写一些猜测,比如经典的科幻作品《三体》,大家为什么觉得这本小说非常有趣呢?
我刚才提到了,因为三体问题无法用经典方法把解写出来。三体是一个混沌系统,最重要的特征是不可预测。三体的运动,假如时间不够长,是不可能预测未来会如何变化。
《三体》小说就是利用这种特征,描述了一个世界有三个太阳,三个太阳的运转处于非常不可预测的状态,可能三个太阳突然出现,使星球上的所有生命热死,很可能三个太阳一段时间都不出现,让星球很冷,把所有生命冻死,这就是《三体》小说里的科学原理。
对人类而言,我们没必要担心太阳系是否稳定,科学家计算过,几百万年,甚至上亿年内都没有问题,即使不稳定,也要几亿年后才会出现的事了。
人类为什么要关心太阳系的稳定性呢?我想说科学的发展并不是从实用性的角度出发的。现代科学从牛顿力学而来,牛顿力学又从天体力学而来,而天体力学刚开始是满足人类的好奇心,但是科学给人类的生活带来革命性的发展与技术不一样,技术是竞技性的,科学是革命性的,现代的生活,所有一切是由于科学的发展,故而用功利性的眼光去看科学研究是错误的。

数学家有一个非常深刻的理论,叫KAM理论(编者注:KAM理论是经典力学里讨论近可积保守系统:哈密顿系统,可逆系统,保体积映射的动力学性态的著名的理论。K ,A,M 分别代表公认的于上个世纪五六十年代创立该理论的三位数学家,他们是:俄罗斯数学家 Kolmogorov和 Arnold,以及德国数学家 Moser),有很多数学家为此做出了很大的贡献。
人们对力学系统所关心的问题之一,是运动过程的长期行为和它最终会达到的状态。动力系统的长时间行为可能有多种形式:平衡或不动点、周期振动、准周期运动、混沌,它们都是定常态。
牛顿力学的确定论观点曾因解决太阳系行星运行问题的成功而在很长时期占统治地位,但是,力学中的三体问题和重刚体绕固定点的运动问题成为困扰人们近一个世纪的难题,KAM定理通过对弱不可积系统运动稳定性条件的证明,说明了三维以上非线性系统的运动轨道出现混沌现象具有普遍性。
稳定性的对立面就是混沌,认知的进步使我们认识到世界越来越多元,越来越发现稳定性的可能性不大,大部分情况是动态的稳定,或者是混沌的系统。
庞加莱:第一个描述混沌的科学家

上图是挪威的皇帝奥斯卡二世,这是唯一的一位数学家皇帝,本科读了数学,一直喜欢科学和艺术,定期在皇宫组织科学讲堂。他在位时,创立了一本数学杂志:《Acta Mathematica》,现在仍是数学领域的四大杂志之一。
1887年,有一位数学家Mitag Lefler建议他设立一个科学大奖:谁能解决三体问题,就把这个奖颁给他。虽然现在我们知道三体问题不可解,但当时大家并不知道。
Mitag Lefler何许人也?我给大家讲一个故事,诺贝尔奖为什么没有数学家呢?传说是因为诺贝尔的情人被一位数学家拐骗走了,那位数学家就是Mitag Lefler。

1895年,皇帝请巴黎大学的数学家潘勒维到皇宫做讲座,当时潘勒维提出了一个猜测,现在叫潘勒维猜测,该猜测经过不到一百年,最后在我的博士论文里面用混沌问题得出了解。

大家可能要问为什么会花这么长时间呢?因为我们对科学的理解是一步一步发展的,庞加莱跟潘勒维是同期的数学家,其实我证明的猜测是庞加莱和潘勒维共同探讨的猜测,庞加莱写了关于如何解三体问题的一篇文章,虽然并没有解出来,但是获奖委员会最后还是决定给了他一个大奖。但有意思的是结果他的学生发现文章里面有错误,庞加莱又重新写了一篇文章,在这篇文章里,混沌的概念第一次在数学里被正确描述。
混沌最基本的概念:几何级的增长速度特别快


下面这个故事相信很多人都听过,一位数学家发明了国际象棋,皇帝非常高兴问他想要什么样的奖赏,数学家说很简单,你在棋盘里面第一格放1颗麦子,第二格放2颗麦子,第三格放4颗麦子,第四格放8颗麦子,再下面一格放16颗麦子,用这种方式把棋盘放满就够了。
皇帝认为数学家的要求不是很高,只不过要了几颗麦子而已,当即答应了。实际总共需要多少颗麦子呢?棋盘一共是64格,第一格是1,最后一格是2的63次方,一共是2的64次方减1,大约是140万亿升的麦子。由此可见,几何级的增长速度特别快,这也是混沌里最基本的一个概念。


我们看上图这个盒子,一个盒子里面放入气体分子,分子在盒子里运动速度非常快,假如有一个小的误差,第一秒就加倍,第二秒又加倍,第三秒又加倍,60秒后,2的60次方,原先再小的误差都被刚才的这种方式加倍,由此可见,分子运动带来的后果是非常大的,而混沌的量有多少,取决于多长时间加倍一次。

在空气动力学中,空气移动比较快,可能零点几秒钟就加倍。太阳系运动相对较慢,误差加倍时间可能需要几十年、几百年,但有一个共同的性质存在,误差在一次一次的加倍!时间拉长后,你没法知道它原先的状态,因为一次次加倍带来的后果是将来不可预测,这就是将来不可预测原理。
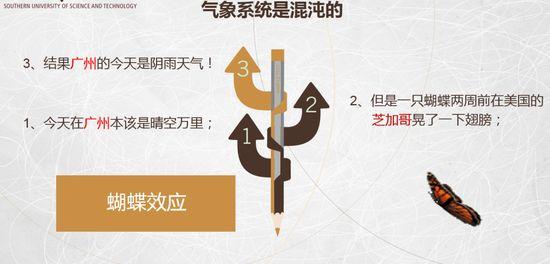
气象系统是最典型的混沌系统。大家可能都遇到过,准备周末出去玩,一看气象预报是晴天,到周末却开始下大雨,大家可能都会指责气象台预报的不准,事实上气象是一个非常混沌的系统,基本没有办法长时间预测。
本来广州应该晴空万里,但有一只蝴蝶在美国芝加哥挥了挥翅膀,它对空气的影响可能一秒钟以后就会加倍,两个星期以后就会影响着广州的气候。
这就是蝴蝶效应,也是为什么说气象系统是典型的混沌系统,假如要想精确预告天气,你必须知道芝加哥的每一只蝴蝶在两个星期之前干了什么,但有很多比蝴蝶更大的影响因素,比如汽车、飞机、人,想预告广州两个星期后的气候,就必须知道在地球另外一边发生的所有现象,这几乎是不可能的,所以短期气象预告可以的,但长期只能从概率上去预告。
混沌究竟是好还是坏?
大家都知道混沌非常地糟糕,那是不是就代表着不好?我讲一个代表混沌系统好的例子。现在中国、美国、印度等国家,大家都想进行太空探测,上月球、上火星,所以要发射很多卫星探测器。

1991年4月,日本发射了HiTen的月球探测器,上天后才发现燃料不够,大家可能觉得这种问题不应该出现,这是因为发射过程有很多不定因素,放太多的燃料,重量就会增加,多放一斤燃料就要少放一斤科学仪器,而燃料刚好够,但是遇到特殊情况就可能出现燃料不足的情况。美国加州理工大学JPL实验室,派了一位数学家叫Belbruno,协助日本人重新设计轨道。

解决方案是利用有限的燃料把探测器送到混沌区域,混沌区域的将来不定,可能会出现在任何地方,到达有利地点就让它过去,不利的地点就稍微花一些燃料推动一下,1991年10月份,科学家用这种方式,最后成功地把探测器送到了月球轨道。
某一天Belbruno给我打电话,说读了我的一篇文章,他在找混沌区域时,花了一个月的时间,如果先读了我的那篇关于混沌的文章,可能不用一个月就可以很快找到相应的区域,我听后非常高兴,没想到自己发表论文居然会有所应用。
本来以为这种事情日本发生了一次,以后就不太可能再发生了。谁知7年以后,1998年美国Hughe公司的一个探测器也遇到了同样的问题,发射后发现燃料不够,这时他们又找道Belbruno,很快,Belbruno帮他们重新设计了一条新的轨道,让探测器又成功抵达了原先的轨道。(注:文字信息未经夏志宏审校,图片来源于夏志宏演讲PPT)
在GMIC会场,新浪科技就数学的发展、本科生数学教育如何培养、交叉学科研究等问题专访了夏志宏教授。
新浪科技:您认为数学在中国科学中处于什么样的地位?近期四部委发布《关于加强数学科学研究工作方案》的文件,您是怎么看待这个方案的?
夏志宏:我注意到这个消息,这是个非常大的事,也是非常好的事。
中国对基础科学非常关注,但对数学的投入还是少了些,数学是所有学科的基础,尤其数学对提高大众的社会素质非常重要,它包含着分析能力、逻辑推理能力、简单的抽象思维能力,对公民素质的评价非常重要。
我经常举好多简单的例子,经过数学推理逻辑思维培训的人有很多方面的优势,对分析能力、以后的发展都非常有用。数学教育的一个误解是希望培养专业的数学家,其实数学教育不仅仅是培养数学家,这只是小小的一部分,数学素质的培养是对整个民族素质,不仅是理工科的,对文科都是非常重要的。
国家现在开始重视数学教育,作为一个数学家我觉得非常高兴,这是一个非常大的机遇,也是一个很大的挑战。
挑战是什么呢?国家人才的培养应该是多层次的,鼓励做研究本来是好事,但数学教育不仅仅是研究,有些学校没有足够的研究水平和能力,但也在拼命追求写文章,做一些毫无意义的研究工作,而且以论文作为一个指标,这样对于整个数学的发展是很不利的。
另外一个挑战,国家会投入更大的财力物力去支持数学研究,我希望看到的是更多支持年轻的、非常活跃的一些数学家,把资源充分地给他们,鼓励他们研究。
资助的方式也应该有很多不同的层次,除了政府还有民间,政府有不同的机构,资助的方式也不一样,可以多元化一起来做。
新浪科技:现在很多前沿研究都属于交叉的学科,因此产生一种说法,认为数学是学好其他学科的基础,您是怎么看待这个说法?
夏志宏:数学研究本身非常重要,但数学教育启发学生的好奇心,对于任何学科都有帮助,它作为所有学科的基础,尤其逻辑推理能力、分析应用能力以及量化分析能力、抽象思维能力,这些都是一些基础素质,比方说你想做好物理、工程,哪怕做社会科学,都需要这些简单的技能。所以提高数学研究,提高数学老师本身的数学培养,这样可以提高学生基本素质。
谈公民素质的时候我一直想强调公民的数学素质,一个社会的进步依赖于所有的公民有比较好的各方面素质,但数学素质往往可能是被忽略的。
新浪科技:不管是数学,一种新的研究成果出来,民众更感兴趣的是这个研究成果有什么用,以后能应用到什么地方,面对科学功利化,您怎么看?您又是怎么看待应用数学研究和基础数学研究之间关系?
夏志宏:应用研究和基础研究没法人为地分开,有些数学研究刚开始是没有任何应用,也看不出任何的应用,比方说现代科学的起源,是从牛顿开始的,你可以说牛顿仰望星空去看行星的运动,是一件很不着边际的事,但就是牛顿跟科学家们,对一些大家觉得可能觉得毫无实用价值的科学研究,带来了现代科学的发展,而现代科学对人类的文明、生活带来的影响是巨大的,现代科学都是从无用开始的,到现在才变成现代生活完全不可或缺的部分。
还有,数论可能大家觉得是一个毫无用处的学科,为什么关心数数,为什么要关注几个数字之间的规律,但是没有数论就没有现代的编码学,就没有现在的因特网,现在网络所有的交流、基本的保密加密方法都是从数论中来的,没有数论就没有办法在网上做任何交易,因为没有办法使网上的交易能保密,这是数学非常妙的地方。
新浪科技:这种美妙的事情是不是可以认为是数学里潜在的美学价值,普通人可能学数学,看到一堆公式觉得很枯燥,作为一个数学家您是怎么看待这种美学价值?
夏志宏:这种美学价值不是生来俱有的,一方面美是一开始就有,这是慢慢对数学的研究、对数学进一步了解以后会看到,比方说对称性,比方说非常美妙的剪辑方法来描述整个世界,比方说爱因斯坦的场方程就是非常美妙的数学方程,这种美真正要你进入后慢慢培养,跟现代艺术也有类似的地方,要沉浸进去,要有充分的了解,是后天培养出来的。
新浪科技:学好数学有什么秘诀吗?如果要成为一名数学家,需要数学方面有天分,还是说通过后天的努力也可以达到?
夏志宏:数学有好多方面,而每个人的技能也是不一样的,不要认为某一方面不行可能数学就不行,数学面非常广,如果代数、抽象的公式不行,但是你可能几何很好,或者空间概念很好,我相信大部分人都可以找到所能激发他兴趣的某个方向的。
抽象思维是需要慢慢培养的,很多人数学学不好是没有适应抽象思维的方式,没有进入的足够顺利,我想大家其实都有简单抽象思维的能力,人要抓住一个事情的本质,需要把它抽象出来,需要把它简单化,这样才能真正地看透这些事情。
新浪科技:您在美国和中国的大学都任过教,不知道您对中国和美国大学的培养方式有什么不同的看法?
夏志宏:美国的培养方式更注重的是学生的兴趣,中国的培养方式是注重技巧和基本技能,我们国家对学生培养的过程,是让学生花很多时间去演算,而美国学校的教育更多是启发学生,所以在考试的时候美国学生绝对考不过中国学生。
但美国学生假如想做数学,他是真的对数学感兴趣,即使告诉他将来会非常辛苦,他仍然去做。中国有时虽然你也感兴趣做数学,但是更多的情况下,一个更好的机会你可能就去做其他东西了。
所以大家都在问为什么开始考试的时候都很厉害,做研究的时候反而不是那么特殊,当然中国也有很多非常优秀的中国科学家,但是相比我们整体的中学教育和考试的水平,这个数字相对少一些。
新浪科技:2019年7月20日是阿波罗工程登月50周年,前段时间中国也宣布火星车已建好,印度也发射了月船2号探测器,世界各国掀起了新一轮的外太空探索热潮,您对天体方面的研究也比较多,您觉得遥远的天体研究对于目前的外太空探索有哪些帮助或指导意义?
夏志宏:一个人对外太空或天文的兴趣是一种求知欲,这种兴趣是人类智慧的一个特征,对未知事件的探索,正是因为这些科学使人的生活更丰富,科学探索从物质上也许没有用,但对人的心理是非常有用的。我们知道一些好像不实用的知识,但这些知识满足了我们的求知欲。所以科学永远是满足求知欲,对未知事物的探索,无论有无用,对科学家来讲这也是一种感受,这并不亚于物质享受,未必比一顿美食要差。
从另外的角度,因为这种探索有时候给我们一些惊喜,突然发现有很多用处,现代科学的发展也证明了这一点,我们对世界的探索给我们带来了很多有用的东西,也许现在登月计划可能没有多少物质上实用的东西,但对整个人类的精神上的满足不容忽视,它是一个非常重要的事件。
科学的发展从开始无用,突然发现有很多有用的东西,然后花更多的精力去做有用的研究,例如又再次返回太空去进行火星计划、月球计划,这是一个好的回归科学,人类再给自己一个挑战,看我们能做些什么,这也许是没有用的,但也许又会给将来科学发展新的推动。
人类作为共同体,大家接受这种挑战,而且各个国家,不仅是中国,美国、印度,都在主动地接受挑战,这对于科学发展来讲是一个非常好的事情,也是一个非常好的机遇。
新浪科技:看到您出席过很多类似于GMIC这样的学界和商业界间的交流大会,您觉得什么原因吸引到您?您觉得科学家在产业界和学界之间扮演着哪种角色?发挥什么样的作用?
夏志宏:科学家跟企业家在一起参加活动,这是一个非常好的现象,现在企业家们对科学关心得比较多,企业家谈的都是非常基础的数学,中国企业家们非常关心中国科学发展,也对基础科学感兴趣,企业家毕竟是中国新兴的一个群体,这个群体对科学能做出贡献,在美国很多私立大学主要的经济来源是捐赠,比方说哈佛大学他们有300多亿美元的基金是完全捐赠的,我所在的西北大学大概有100多亿的捐赠基金,这些基金就是来支撑学校,在美国私立学校的发展主要是依赖于这些捐赠资金。
我国的私立大学西湖大学,也接受社会捐赠,用全民的力量来办一个研究型的大学,我希望西湖大学能发展起来,有更多的企业家关注、去捐赠促进大学的发展。
本文经授权转载自微信公众号“新浪探索”。
特 别 提 示
1. 进入『返朴』微信公众号底部菜单“精品专栏“,可查阅不同主题系列科普文章。
2. 『返朴』提供按月检索文章功能。关注公众号,回复四位数组成的年份 月份,如“1903”,可获取2019年3月的文章索引,以此类推。
《返朴》,科学家领航的好科普。国际著名物理学家文小刚与生物学家共同出任总编辑,与数十位不同领域一流学者组成的编委会一起,与你共同求索。关注《返朴》(fanpu2019)参与更多讨论。二次转载或合作请联系返朴公众号后台。
,




