平面几何中的面积其实代表图形的占地大小,那么如何才能更好地表示面积呢?
考虑到,一条线段在与其垂直的直线上的投影为零,也就是说不存在分量,两个相互垂直的变量最适合表示平面几何图形的大小。面积代表图形在平面中所包围的区域大小,平面几何图形面积的求法其实就是转化为两个相互垂直的变量乘积。

矩形是最容易求面积的图形,因为其相邻两边均是互相垂直的,所以可以直接进行那么其面积S=ab
其他图形面积计算一般需要将其转换为矩形来求面积。
平行四边形往边长a上做垂线h,可将其拼成底为a、高为h的矩形,其面积就为S=ab
对于三角形,可将两个同样的三角形拼成一个平行四边形,那么三角形的面积就可转换为平行四边形的面积的一半,其面积
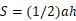
梯形面积求法与三角形类似,将两个相同的梯形拼接成平行四边形,那么梯形的面积也可看作对应平行四边形面积的一般,其面积为

对于扇形,可将其看作无数个小三角形叠加而成,这些三角形的高均为半径r,那么其面积就相当于一个底为弧长l、高为半径r的三角形面积,

圆形可以看作是一个角度为360°(弧度为2π)的扇形,那么其面积为

从这些图形的面积的求法的过程就可以看出数学中推导转化的重要性,这些复杂图形的面积最终都可以转换为最简单的矩形面积求法。
,