时间最久未解决的数学世界难题（世界难题四色猜想首次数学直接证明）

四色问题：又称四色猜想、四色定理，是世界近代三大数学难题之一。地图四色定理（Four color theorem）最先是由一位叫古德里（Francis Guthrie）的英国大学生提出来的。四色问题的内容是“任何一张地图只用四种颜色就能使具有共同边界的国家着上不同的颜色。”也就是说在不引起混淆的情况下一张地图只需四种颜色来标记就行。用数学语言表示即“将平面任意地细分为不相重叠的区域，每一个区域总可以用1234这四个数字之一来标记而不会使相邻的两个区域得到相同的数字。”这里所指的相邻区域是指有一整段边界是公共的。如果两个区域只相遇于一点或有限多点就不叫相邻的。因为用相同的颜色给它们着色不会引起混淆，如下面这个128国的涂数。

如果用世界最快的计算机每秒5.1*10的17次方计算， 128国大概需要10的55次方年，也就是说暴力破解基本无解（通过本证明方法求解，应该30分钟可以解决）。公布一组正确解，如下图：

如果你想了解上图的涂数是如何填入的，请跟我一起来开始四色猜想的证明旅程吧，过程相对枯燥，阅读需要耐心。

证明思路：任何一个国家的形状都可以由圆形变形而来，我们假设这个国家为A，而任何一个平面和球面地图我们都可以从A国开始往外增加国家做出这幅地图，所以只要推导从A国开始再增加1到x国，无论是增加的国家还是其外延始终小于等于4，那么就可以直接推导出任何平面和球面地图都只需要用4色就可以涂成。

定义：外延为图一中的Y（如图一所示）：在球面地图中Y是除封闭A外的剩余部分，Y就犹如地球的海洋，有陆地就必然有海洋，所以在球面内Y是A永远无法抵达的部分；在平面地图Y就相当于做平面地图的涂布，所以Y也是永远无法到达边缘的。因此对于球面地图或者平面地图，都可以用图一表示，而Y都是它们无法触及的部分。

证明过程（1、2、3、4表示四种颜色）：

第一步：任何一个平面或者球面只有两国，必两国最多只有一条边重合。

如图所示：A=1，Y=2，重合的一条边为红圈。

第二步：任何一个平面或者球面只有三国，两两之间最多只能重合两条边。

如图所示：A=1，B=2，Y=3，与外延Y重合的两条边分别为红线和蓝线。

第三步：任何一个平面或者球面只有四国，两两之间最多只能重合三条边。

证明过程：

当形成第三国C国的fd线（黄线一飘）的d点在A国的fb线（红线一飘）除f点上时，C国涂色最小为C=2，此时：A=1，B=2，Y=3；当形成C国的fd线（黄线一飘）的d点在第二国B国的bc线（蓝线一飘）或者在A国的cf线（红线二飘）除b点的位置时，第三国C涂色最小为C=3，此时：A=1，B=2，Y=4。所以其最小涂色的最大数情况为A=1，B=2，C=3，Y=4，与外延Y重合的三条边分别是红、蓝、黄线。

第四步：任何一个平面或者球面只有五国，两两之间最多只能重合四条边。

证明过程：

当第三国C国的fd线（黄线一飘）的d点在A国的fb线除f点上时，第三国C国涂色最小C=2，此时：A=1，B=2，Y=3；当形成第三国C国的fd线（黄线一飘）的d点在第二国B国的bc线（蓝线一飘）或者在A国的cf线（红线二飘）除b点的位置时，第三国C国的涂色最小为C=3，此时：A=1，B=2，Y=4，故我们以第三国的最小涂数的最大数为推导前提。如果以最小数为前提推导，增加第四国就相当于增加第三国，属于倒退现象无意义。这里我们假设C=3。

因此当形成第四国D国的eh线（粉线一飘）的h点在A国的ef线（黑色一飘）除e点上或者第三国C国的fd线（黄色一飘）上时，第四国D国的涂色最小为C=2，此时：A=1，B=2，C=3，Y=4；当形成第四国D国的eh线（粉线一飘）的h点在第二国B国的dc线（蓝线一飘）除d点或者在A国的ce线（红线二飘）的位置上时，第四国D国涂色最小为D=4，此时：A=1，B=2，C=3，Y=3。与外延Y重合的四条边分别是红、蓝、黄、粉线。

第五步：任何一个平面或者球面只有六国，两两之间最多只能重合四条边。

证明过程：

根据第五步的情况，我们推导下一国的涂色数，必须以上一国的最小涂数的最大数为前提，否则属于倒退，所以我们假设D=4。

当形成第五国F国的zj线(绿线一飘)的j点在A国的ze线（黑色一飘）除i点上或者第四国的eh线（粉线一飘）上时，第五国F国的涂色最小为F=2，此时：A=1 ，B=2，C=3，D=4，Y=3；当形成第五国F国的zj线(绿线一飘)的j点在第二国的hc线（蓝线一飘）除h点或者在A国的cz线(红线双飘)的位置上时，第五国F国最小涂色为F=3，此时：A=1 ，B=2，C=3，D=4，Y=4，与D国重合的四条边分别是红、蓝、黄、绿线。

第六步：如6图所示，再增加X国，X-1国为最大涂数时，X国的涂色总在2、3、4的范围内变化。当X-1国等于4时，如X=2，那么Y=3；如果X=3，那么Y=4。当X-1国等于3时，如X=2，那么Y=4；如X=4，那么Y=3。当X-1国等于2时，如X=2，那么Y=3；如X=3，那么Y=4。因此X和Y始终小于等于4。

第七步：根据以上结果可以证明与A国相邻再增加无限国家，X和Y都小于等于4。我们以此为结果推导多层复杂结构的四色问题。

一、Y1=2

A、当Y1=2时，新增国Xn与已有国没有重合边：

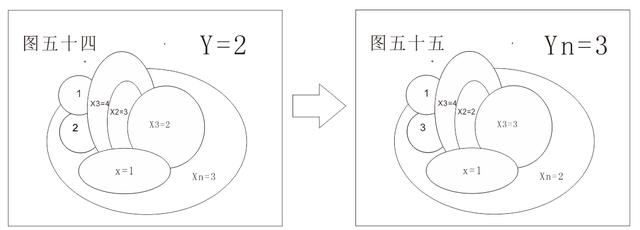
如图所示，当Y1=2，再增加的Xn都等于1，Yn始终等于2，并且国与国之间没有重合边或点，呈现一种气泡状。我们将之称为经典情况，也为它命名为经典情况一。

B、当Y1=2时，新增国Xn与已有国只有一条边重合：

如上图所示，当Y1=2时，除了上一种经典情况必然发展到Yn=3。当增加国Xn仅有一条边与X1国重合时，Xn=Yn-X₁(X₁为Xn与已有国重合边涂数)，Yn始终等于3。Xn呈1和2循环的单链态向外可以无限延伸。在球面和平面内两链之间无重合边或点。因此，这种链式状态我们称之为经典情况二。

二、Y1=3；

A、当Y1=3时，新增国Xn与已有国只有一条边重合：

情况一：

情况二：

如图所示，当增加国Xn只有一条边与已有国重合时，Xn=Y1-X₁(X₁为Xn与已有国重合边涂数)。此种情况Yn=3，结构呈发散之势，在球面和平面内两两发散链之间无重合边或点，此种情况属于一种经典情况，我们为它命名为经典情况三。

B、当Y1=3时，新增国Xn与已有国只有二条边重合：

如图所示：当增加的X3国有两条边与已有国家重合时，X3=3，Yn=4。从X4增加到Xn国的情况下，Xn=10-X₁-X₂-Yn(X₁和X₂为重合边两国涂数)，Yn始终等于4。Xn向外延伸，在球面和平面内无重合边或点。此种情况属于一种经典情况，我们为它命名为经典情况四。

三、Y1=4 ；

A、当Y1=4时，新增国Xn与已有国只有一条边重合：

情况一：

情况二：

如图所示：当增加的Xn国只有一条边与已有国家重合时，Xn=Y1-X₁（X₁重合边国家涂数）。当X n-1≤2时，此时用Y=3求解Xn。Yn始终等于4；当此时Xn等于1或者等于2，在单链上会呈1和2的交替循环，结构呈发散之势，在球面和平面内两两发散链之间无重合边或点，属于一种经典情况，我们称它为经典情况五。

B、当Y1=4时，新增国Xn与已有国只有二条边重合：

如图所示：当增加的Xn国有两条边与已有国家重合时，Xn=10-X₁-X₂-Y1(X₁和X₂为重合边两国涂数)。Yn始终等于4，且呈发散之势，在球面和平面内两两之间无重合边或点，属于一种特殊情况，我们称它为经典情况六。

C、当Y1=4时，新增国Xn与已有国只有一条或二条边重合：

如图所示：当增加的Xn国只有一条边与已有国家重合时，Xn=Y1-X₁（X₁重合边国家涂数）。当X n-1≤2时，此时用Y=3求解Xn；有两条边与已有国家重合时，Xn=10-X₁-X₂-Y1(X₁和X₂为重合边两国涂数)。Yn始终等于4，且呈发散之势，在球面和平面内两两发散链或面之间无重合边或点。属于一种特殊情况，我们称它为经典情况七。

D、当Y1=4时，新增国Xn与已有国有三条边重合：

如图所示，当X4与已有国家有三条边重合时，Xn=Y1，Yn=10-X ₁-X ₂-Y1（Yn为新的外延，X ₁和X ₂是与Xn有两条边重合的国家涂数）。而当Y=1或者Y=2时，如图二十、图二十三和图二十六属于同构体，都可以把Y变换成3，然后从外到内反推已有国家涂数如图所示，此时所有国家涂色依然小于等于4。又因为图二十、图二十三和图二十六也是我们推论的第一步到第七步已经推论出的以A国为中心形成的最复杂体的一个单元。所以我们也以图二十为我们开始多层结构推论的基本单元。

四、基本单元Y1=3：

A、当Y1=3时，新增国Xn与已有国只有一条边重合：

情况一：

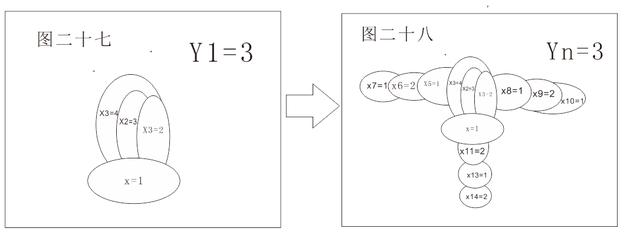
情况二：

如图所示，当增加国Xn的一边与已有国家重合时，当Y1＞X ₁时Xn=Y1-X ₁；当X ₁＞Y1时 Xn= X ₁-Y1（Y为运算中的外延，X ₁是与Xn有两条边重合的国家涂数）。Yn始终等于3，Xn在1和2之间循环，结构呈发散之势，在球面和平面内两两发散链之间无重合边或点。属于一种经典情况，我们称它为经典情况八。

B、当Y1=3时，新增国Xn与已有国只有二条边重合：

如图所示：当增加国Xn的二边与已有国家重合时，Xn=10-X₁-X₂- Y1 (X₁和X₂为重合边两国涂数)，Yn始终等于3，如上所示此种结构Xn呈双链状态向外延伸，在球面和平面内双链之间无重合边或点。此种情况属于一种经典情况，我们为它命名为经典情况九。

C、当Y1=3时，新增国Xn与已有国有三条边重合：

如图所示：当新增国Xn有三条边与已有国重合时，Xn= Y1=3，当Y1＞X ₁时Y=Y1-X ₁；当X ₁＞Y1时Y= X ₁-Y1（Y为运算中的外延，X ₁是与Xn有两条边重合的国家涂数）。又因为实际与外延接触的国家只有两个，所以我们可以把Yn替换成3，然后从外到内反推已有国家涂数如图所示，依然X1到Xn小于等于4。此种情况循环到了二的B情况。

D、当Y1=3时，新增国Xn与已有国有一条或两条边重合：

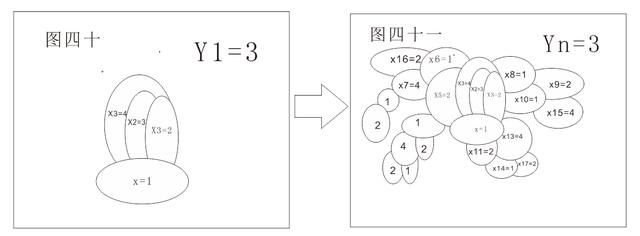
如图所示，新增国Xn与已有国重合边为1时，当Y1＞X ₁时Xn=Y1-X ₁；当X ₁＞Y1时Xn= X ₁-Y1；当新增国重合边为2时，Xn=10-X₁-X₂-Y1(X₁和X₂为重合边两国涂数)；或者1和2交替出现，Yn=3不变。如上所示此种结构Xn向外发散之势，在球面和平面内双链之间无重合边或点。此种情况属于一种经典情况，我们为它命名为经典情况十。

E、当Y1=3时，新增国Xn与已有国的重合边为一个集合{1、2、3、4…N}，此时如果X4≠3，就可以一直往外推演。如果X4=3，则循环到了C种情况。

此种情况下有三种情况：

定义：设增加Xn-1国后整个图形与外延重合的边总数为Z。Xn与已有国重合的边总数为Zn。

1、当Zn=Z时，并且在Z边有两处重合，如图所示；

此时，Xn=Y1，当Y1＞X ₁时Y=Y1-X ₁；当X ₁＞Y1时Y= X ₁-Y1（Y为运算中的外延，X ₁是与Xn有两条边重合的国家涂数）。当Y=2，转换成Yn=3，如下图所示：

方法：将Xn与X1形成的圈内所有的2换成3，3换成2皆可。

当Y=1，转换成Yn=3，如下图所示：

方法：将Xn与X1形成的圈内所有的1换成3，3换成1皆可。

2、当Zn=Z时，并且在Z边只有一处重合，如图所示；

此时，Xn=Y1，Y=10-Xn-X1-X2。（Y为运算中的外延，X ₁和X₂是与Xn有两条边重合的国家涂数）

当Y=4，转换成Yn=3，如图所示：

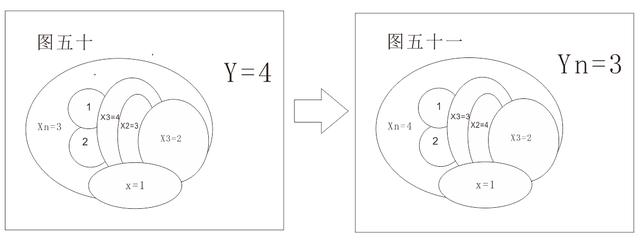
转换方法：将Xn与X1形成的圈内所有的4换成3，3换成4皆可，此时Xn=4。

当Y=1时，转换成Yn=3，如图所示：

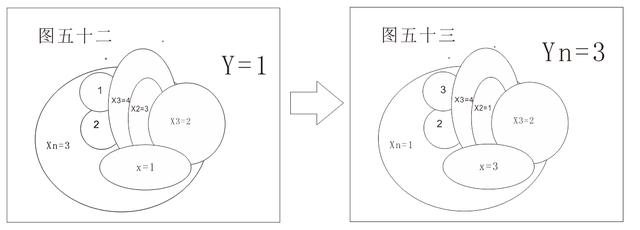
转换方法：将Xn与X1形成的圈内所有的1换成3，3换成1皆可，此时Xn=1。

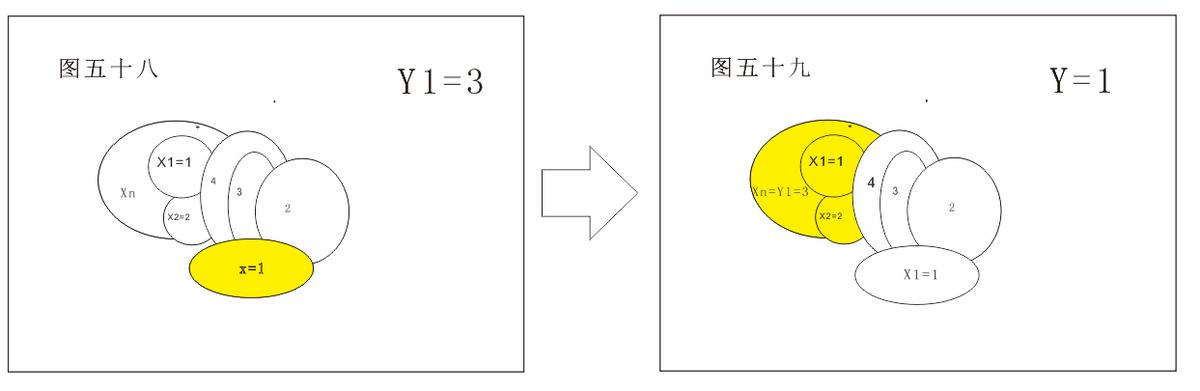
当Y=2时，转换成Yn=3，如图所示：

转换方法：将Xn与X1形成的圈内所有的2换成3，3换成2皆可，Xn=2。

3、当Y=3， 3≤Zn＜Z，如图所示：

当X1≠X2，Yn=10-Y-X1-X2，Xn=Y1=3，Y=10-3-2-4=1

因为Y=1，与已有国总和的边缘国冲突（上图标黄国）

所以Yn与已有国的边缘相同时，不能将已有国所有的涂数进行变化，而只能变化一部分。

定义：国家的总和，我们称为内延，用字母N表示；

定义：当3≤Zn＜Z ，Xn=Y1，此时以Xn为中心向内延N延伸，所有与Xn相交涂数等于Y(运算中的外延)的国，以及与这些国相交涂数为3的国，以及涂数为3的国的外围涂数为Y1的国，这样不断延伸形成的国的总和定义为小内延T（图中标黄部分）；

此时有三种可能性：

第一种情况：如果T和N重合的部分不能把N分成至少两份（如图五十九中标黄的部分），且X1≠X2时，那么根据调换规律可知：当Xn=Y1=3，Y=1那么就要将T内所有1与3交换，变化后Xn=1，Yn=3；当Xn=Y1=3，Y=2那么就要将T内所有1与3交换，变化后Xn=2，Yn=3；当Xn=Y1=3，Y=4那么就要将T内所有1与3交换，变化后Xn=4，Yn=3即可 ，如下图所示：

第二种情况：如果T和N重合的部分不能把N分成至少两份，且X1＝X2时，如下图所示：

此时，Xn=Y1，当Y1＞X ₁时Y=Y1-X ₁；当X ₁＞Y1时Y= X ₁-Y1（Y为运算中的外延，X ₁是与Xn有两条边重合的国家涂数）。那么根据调换规律可知：当Xn=Y1=3，Y=1那么就要将T内所有1与3交换，变化后Xn=1，Yn=3；当Xn=Y1=3，Y=2那么就要将T内所有1与3交换，变化后Xn=2，Yn=3，如下图所示：

第三种情况：如果T和N重合的部分能把N分成至少两份，且X1≠X2时，如下图所示：

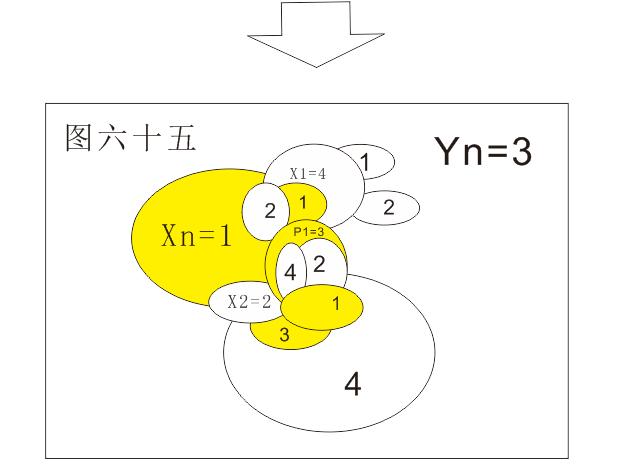
定义：如果T和N重合的部分把N分成至少两份，那么当Yn=3时，重合部分（上图标黄部分）与Yn所有相邻的国涂数为3的国就是突破国，就是Pn，选取任意其中之一定义为P1（如上图六十五）。

这时P1=Yn，四色猜想不成立，是否存在一个变换始终不会产生Pn，那么四色猜想就一定成立。

以下证明经过变换始终不会产生Pn。

定义：T把N分成两个独立的部分，T由Xn和P1组成，所以分成的两个部分定义为D1和D2。如图六十五所示，交换D1中的2和4的位置，不会影响D2的2和4的位置。如下图所示：

X1由原来的4变成了2，此时X1=X2=2并且X1和X2必然相等。

当Xn=3，Y=10-Y1-P1-P2=4，当Yn=3，再把新T内的把Xn变成4，4变成3即可，如下图所示：

证明如图六十八所示：当X1=X2=2，P1=1，Xn=10-Y-X1-P1=4，将T内所有的4变3，3变4后，如果从X1到X2有一个1和2两个涂数不断交互相邻组成的国的集合定义为R1，R1如果必将N能分成两份（如下图所示标红的部分），那么四色猜想就可证。

如图六十九中所示，当Xn=4，R1存在时，四色猜想必成立；但是有一种情况下1和2是不相邻的，就是1和2国被4国隔离，如下图七十所示：

定义：当Xn=10-X1-P1-Y1，Yn=3时，将新T内3变成Xn，将等于Xn的国变成3后，如果D1和D2内有等于3的国与Yn相邻，就是Kn。如果有n个Kn选取D1和D2内最靠近P1的两个分别定义为K1和K2（如上图七十一所示）。

定义：当Xn=4，P1=1之间涂数等于1和4彼此相邻又与Xn和P1相邻的国的总和定义为S1；当Xn=4，K1=3之间涂数等于3和4彼此相邻又与Xn和K1相邻的国的总和定义为S2。在S1和S2之间形成的国的总和包括S1和S2，定义为J。

定义：当P1=1，K1=4时，如果J内能够找到一个国家集合是2和3组成我们叫它R2，并且能够把J分成两个部分，一个部分含P1定义为D3，一个部分含K1定义为D4。那么将D4内的4和1交换位置，就可以使X1=2到X2=2之间再次形成一个1和2交互出现的新的国家集合，即R1依然存在。如下图所示：

现在我们要证明J内必然含有一个国家集合R2把J分成两个部分，一个部分含有P1的叫做D3，一个部分含有K1叫做D4。

证明：如果J内含有2个及2个以上涂数等于4的国家，J与外延Y1和Xn相邻的国必然是1、2、4交替出现三个涂数国，所以J的内部存在不被涂数为1的国家覆盖的情况下（如果存在就是边缘为1、2,不影响推导）等于2的国家与Xn和Y1相邻（如图七十一所示标蓝部分）。又因为所有涂数为3的国家必然与涂数为2的国家相邻，所以在J的内部必然存在一个由2和3组成的国家集合R2把J分成两份，一份含有P1就是D3，一份含有K1就是D4。

然后将D4内的1变成4，4变成1，而在J内所以的2和1必然相邻，所以在N内经过两次变化，必然形成一个X1到X2之间1和2相邻的国家集合R1把N分成两份。因为这个国家集合的必然存在，所以四色猜想此时是成立的。

变化结果如下图：

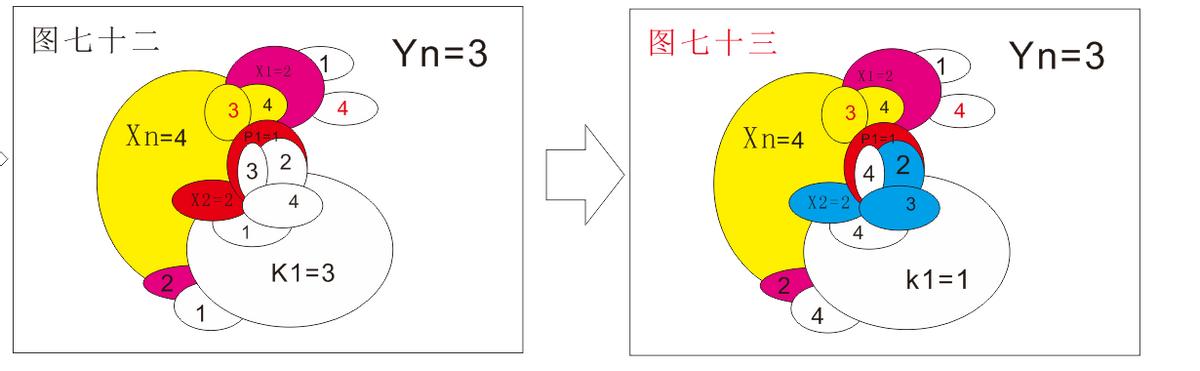
现在要证明，当Y1=3，X1=X2=2，P1=1，K1=4，并且D1或者D2内只有一个涂数等于4，通过相应的变化， R1依然存在，那么四色猜想就一定成立了。如下图所示：

证明： 当Y1=3，X1=X2=2，P1=1,，K1=4，并且D1或者D2内只有一个涂数等于4时，只需要再把D2内的2变成4，4变成2（此时突破国就变成了1和2），再把D4内的1变成4，4变成1即可。在N内同样存在一个R1。（R1是N内由涂数由1和2交替出现的国家集合包含X1和X2，并把N分成两份）此时的Xn=10-X1-X2-Y1=4，Yn=3，再把新T内的3变成4，4变成3即可，如下图所示：

根据以上推论我们做个总结：

当Y=4时，可以推演七种经典情况；

当Y1=3时，可以推演以下所有情况：

Zn=1，当Y1＞X ₁时Xn=Y1-X ₁；当X ₁＞Y1时Xn= X ₁-Y1，Yn=3（X ₁是与Xn有两条边重合的国家涂数）;

Zn=2，Xn=10-X1-X2-Y1，Yn=3(X1、X2为Xn已有国重合边的涂数）;

3≤Zn＜Z，Xn=Y，X1≠X2，Y=10-Y1-X1-X2，当Yn=3时，如果T把N没有分成两份，将T内的Y变成3，3变成Y(Y为运算中的外延)；如果T把N至少分成两份，则有以下三种情况：

1、如果X1=4，X2=2,P1=1时，将D1内的2变成4，4变成2，此时X1=X2,分两种情况，如果存在R1，则Xn=10-X1-P1-Y1=4，Yn=3，将新T内的3变成4，4变成3即可。如果还不存在R1，此时K1必然等于4，如果D2内只含有1个涂数为4的国，则先将D2内的2变成4，4变成2，然后再把D2内的1变成4，4变成1，此时N内必然存在R1，则Xn=4，Yn=3，将新T内的3变成4，4变成3；如果D4内含有2个及2个以上涂数为4的国，直接将D4内的1变成4，4变成1，此时N内必然存在R1，则则Xn=4，Yn=3，将新T内的3变成4，4变成3即可。

2、如果X1=4，X2=1，P1=2时，将D1内的,1变成4，4变成1，此时X1=X2=1,分两种情况，如果存在R1，则Xn=10-X1-P1-Y1=4，Yn=3，将新T内的3变成4，4变成3即可。如果还不存在R1，此时K1必然等于4，如果D2内只含有1个涂数为4的国，则先将D2内的1变成4，4变成1，然后再把D2内的2变成4，4变成2，此时N内必然存在R1，则Xn=4，Yn=3，将新T内的3变成4，4变成3；如果D4内含有2个及2个以上涂数为4的国，直接将D4内的2变成1，4变成1，此时N内必然存在R1，则Xn=4，Yn=3，将新T内的3变成4，4变成3即可。

3、如果X1=2，X2=1，P1=4时，将D1内的,1变成2，2变成1，此时X1=X2=1,分两种情况，如果存在R1(R1由1和4组成)，则Xn=10-X1-P1-Y1=2，Yn=3，将新T内的3变成2，2变成3即可。如果还不存在R1(R1由1和4组成)，此时K1必然等于2，如果D2内只含有1个涂数为2的国，则先将D2内的1变成2，2变成1，然后再把D2内的2变成4，4变成2，此时N内必然存在R1(R1由1和4组成)，则Xn=2，Yn=3，将新T内的2变成3，3变成2；如果D2内含有2个及2个以上涂数为2的国，直接将D4内的2变成1，1变成2，然后再将D4内的2变4，4变2，此时N内必然存在R1(R1由1和4组成)，则Xn=2，Yn=3，将新T内的2变成3，3变成2即可。

3≤Zn＜Z，当X1=X2=1，Xn=2，Yn=3，如果T不能将N至少分成两份，则把T内的2变成3,3变成2；当X1=X2=2，Xn=1，Yn=3，如果T不能将N至少分成2份，则把T内的1变成3,3变成1；当X1=X2=4，Xn=1，Yn=3，如果T不能将N至少分成2份，则把T内的1变成3,3变成1；

如果T把N至少分成两份，则有以下三种情况：

1、如果X1=X2=2, P1=1时，如果Xn=10-X1-P1-Y1=4，Yn=3，此时存在一个R1，将新T内的3变成4，4变成3即可。如果还不存在R1，此时K1必然等于4，如果D2内只含有1个涂数为4的国，则先将D2内的2变成4，4变成2，然后再把D2内的1变成4，4变成1，此时N内必然存在R1，则Xn=4，Yn=3，将新T内的3变成4，4变成3；如果D4内含有2个及2个以上涂数为4的国，直接将D4内的1变成4，4变成1，此时N内必然存在R1，则则Xn=4，Yn=3，将新T内的3变成4，4变成3即可。

2、如果X1=X2=1，P1=2时，如果Xn=10-X1-P1-Y1=4，Yn=3，此时存在一个R1，将新T内的3变成4，4变成3即可。如果还不存在R1，此时K1必然等于4，如果D2内只含有1个涂数为4的国，则先将D2内的1变成4，4变成1，然后再把D2内的2变成4，4变成2，此时N内必然存在R1，则Xn=4，Yn=3，将新T内的3变成4，4变成3；如果D4内含有2个及2个以上涂数为4的国，直接将D4内的2变成4，4变成2，此时N内必然存在R1，则Xn=4，Yn=3，将新T内的3变成4，4变成3即可。

3、如果X1=X2=4，P1=1时，如果 Xn=10-X1-P1-Y1=2，Yn=3，此时存在一个R1，将新T内的2变成4，4变成2即可。如果还不存在R1，此时K1必然等于2，如果D2内只含有1个涂数为2的国，则先将D1内的2变成4，4变成2，然后再把D2内的1变成4，4变成1，此时N内必然存在R1（1、2集合的R1），则Xn=4，Yn=3，将新T内的3变成4，4变成3；如果D4内含有2个及2个以上涂数为4的国，直接将D4内的2变成1，1变成2，此时N内必然存在R1(1、4集合的R1)，则Xn=2，Yn=3，将新T内的2变成4，4变成2即可。

当Zn=Z时，并且在Z边有两处重合，此时，Xn=Y，当Y1＞X ₁时Y=Y1-X ₁；当X ₁＞Y1时Y= X ₁-Y1。当Xn=1，Yn=3时，再将N内所有的1换成3，3换成1皆可；当Xn=2， Yn=3时，再将N所有的2换成3，3换成2皆可;

当Zn=Z时，并且在Z边有一处重合，此时，Xn=Y，Y=10-Xn-X1-X2。当Xn=1 ，Yn=3时，再将N内的1换成3，3换成1皆可；当Xn=2， Yn=3时，再将N所有的2换成3，3换成2皆可；当Xn=4， Yn=3时，把Yn变成3时，将N内所有的4换成3，3换成4皆可；

由上可知当Y=3时，无论增加国是与已有国重合多少边，都可以根据公式继续往外推演。

核心要点：当Yn=3，1≤Zn≤Z时，不管T能不能将N至少分成两份，经过复变，Xn始终大于等于1小于等于4不等于3。

第八步结论：因为在任何平面或者球面上，无论从A国再增加Xn国，七种经典情况Y=4或者有基本单元 Yn=3时，Xn始终大于等于1小于等于4不等于3，所以四色猜想成立。又因为四色猜想成立，所以在任何平面或者球面内，两两国之间最多只能有四条边重合。

后语：

1. 、根据以上四色定理，作任何一幅地图，首先确定这幅地图的基本单元，然后利用公式往外推演；如果没有基本单元，则按照十种经典情况往外推演即可。
2. 四色定理与中国的老子之道相通，因为老子之道的核心思想就是道生一、一生二、二生三，三生万物，与四色定理的推演方式一致。
3. 、当3≤Zn≤Z时，每一次个体增加都会导致整体变化，犹如细胞增殖生命生长。
4. 、当Y1=3，基本单元中与三边相邻的国家涂色为3，然后从12点钟方向顺时针确定1、2、4，然后Zn始终大于等于3，通过本证明推演任何一副地图每一国都有且只有一个涂数结果。这个结论可以帮助我们重新设计一种不同于素数分解的全新的加密方式。
5. 根据本证明推导，三维世界的立方体可以拓扑为两种结构：圆形和圈形，只需7色就可以区分。

备注：此证明于2020年8月15日首发于今日头条，本版本为修正版本

将不准确（如小内延T的定义，如突破国Pn的定义，如R1等）的地方做了必要的修改和补充。

数学爱好者：刘江

2022年2月18日

,