

01---为什么三角尺的锐角设计成特殊角?
三角尺的锐角为什么要做成30°,60°,45°?
---特殊角呗。
---可以很方便画其他非特殊角比如15°,75°等。
---三边之比1:√3:2或1:1:√2。
。。。。。。
这些回答都是对的,但又是不完整的。
下面我们看看,除了大家说的以外,还有哪些原因。
△ABC中,AB=c,BC=a,AC=b,C=90°,

则三边满足勾股定理,
a² b²=c²
即两边的平方和=第三边的平方。
突发奇想:这两边的平方差呢?这两边的平方差与第三边有什么关系?
a²-b²可以用c表示吗?
如图1,若∠A=60°,∠B=30°,∠C=90°,则c=2b,a=√3b

-------图1------
a,b,c三边显然满足勾股定理,
即a² b²=c²,
不仅这样,而且
a²-b²=3 b²- b²=2 b²=2b·b=bc,
即a²-b²= bc.
这个结论对另一块三角尺是否成立?
如图2,若∠B=∠C=45°,∠A=90°,则b=c,a=√2b。
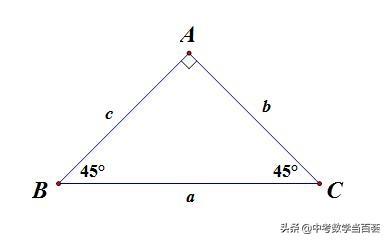
-----图2----
b,c,a三边显然满足勾股定理,
即b² c²=a²,
不仅这样,而且
a²-b²=c²= b·c=bc,
即a²-b²= bc.
这是一般直角三角形所没有的性质哟!
02---倍角三角形及其性质仔细分析产生这一现象的原因:
1.因为直角吗?
显然不是,直角只能保证三边满足勾股定理:两边的平方和等于斜边的平方。
2.因为特殊锐角吗?
含30°或者45°的三角形中,三边也不一定存在这种关系。
3.原因既不是1,也不是2。只能是。。。,再仔细观察发现:图1和图2中,都有“∠A=2∠B”这个条件。即图1中,60°=2×30°,图2中,90°=2×45°。
是不是说,撇开那些特殊角,比如,90°,45°,30°,60°。
只要一个三角形满足:一个角是另外一个角的2倍,三边就有上述关系呢?
试试看,如图3,
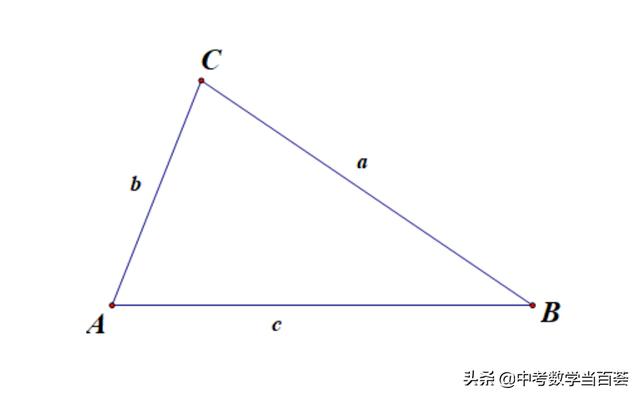
-----图3----
△ABC中,AB=c,BC=a,AC=b,∠A=2∠B,
如图4,作∠CAB的平分线AD,
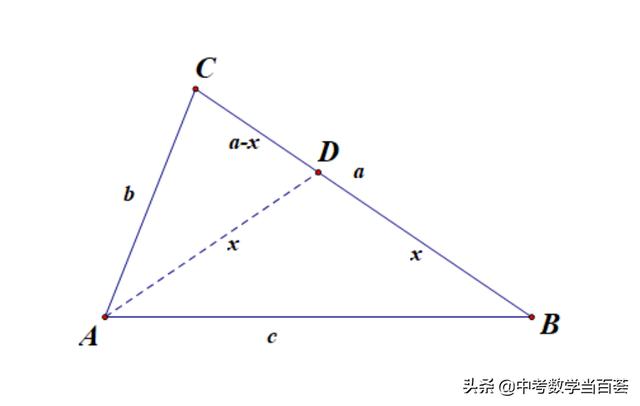
---图4---
则∠DAB=∠DAC=∠B,
所以设DA=DB=x,CD=a-x,
并且在△ACD和△BCA中,
∠DAB=∠B,∠C=∠C
所以且△ACD∽△BCA,
因而三边对应成比例,
即b:a=(a-x):b=x:c
解得x=bc/a,且b²= a²- bc,
即a²-b²= bc.
上述探究过程说明,一个三角形中,若一个角是另一个角的两倍,则这个三角形的三边就存在这种关系。
哪种关系?
试着说明一下:两边的平方差,等于另一边与第三边之积。
这个说法显然含糊不清,不满意!
再来一次。
成倍角的两角所对边的平方差(非负),等于较短边与第三边之积。
因而,我们就有了下面一般性的结论:
倍角三角形的定义:
一个三角形中,若一个角是另一个角的两倍,则这个三角形叫做倍角三角形。
倍角三角形的性质:
倍角三角形的三边满足:成倍角的两角所对边的平方差(非负),等于较短边与第三边之积。
太啰嗦啦!
没办法。要说清楚,只能这样啦!不过对照图看可简洁多了(图形语言多重要哟)。
如图5,△ABC中,若∠A=2∠B,则a²-b²= bc.
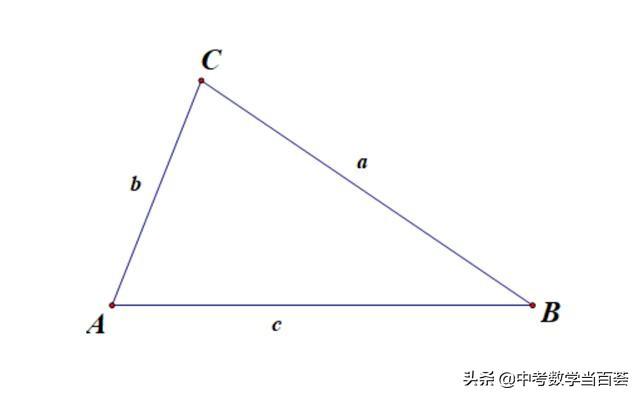
-----图5-----
从这里可以看出三角尺的锐角设计成30°,60°,45°,除了前面大家说的原因外,还有一个重要原因:两块三角尺也是倍角三角形!
常见的倍角三角形,除了两块三角尺以外,还有顶角为36°的等腰三角形(黄金三角形,如下图)。

03---倍角三角形的性质应用举例
这个结论有何用途?
这是大多数最关注的,下面略举三例说明。
例1.△ABC中,∠B=2∠A,且BC=5,AB=10,求AC的长及三个内角。
分析:你看吧,∠B=2∠A,就说明△ABC是倍角三角形,因而其三边应该满足前面总结的那句话(自己画草图,看清楚图哟,哪角对哪边,哪是第三边,可要看仔细,小心列式出错),即得AC²-BC²= BC×AB,代值计算得AC²=75,则AC=5√3,
∵AC² BC²= 100= AB²,
∴△ABC是Rt△,且∠C=90°,
则∠B ∠A=90°,∠B=2∠A,
解得∠A=30°,∠B=60°.
点评:此题重点在画草图和强烈的对应意识!
例2.一个三角形的最大角是最小角的2倍,且三边为连续整数,求三边长。
分析:画草图,此三角形为倍角三角形哟,设a=x-1,b=x,c=x 1,
则
(x 1)²-(x-1)²=x(x-1)
解得x1=0(舍去),x2=5
所以三边长为4,5,6.
点评:同上,画草图和强烈的对应意识!
例3.如图6,△ABC中,∠C=3∠A,BC=27,AB=48,求AC的长.

----图6-----
分析:突然蹦出3倍角,咋办?分割呗!如图7,在AB边上找一点D,连DC,使得∠DCB=∠A,
则∠DCA=2∠A,因而△ACD是倍角三角形,不仅如此,而且△ABC∽△CBD(为什么?卖个关子!)。

-----图7------
因而,
由倍角三角形三边关系得,
AD²-CD²=CD×AC,
由相似三角形三边关系得,AB:CB=BC:BD=AC:CD,
即 48:27
=27:(48-AD)
=AC:CD,
解得AC=35。
点评:比上面多一条,分割构造倍角三角形。
04---结语从特殊三角形(两块三角尺)中,发现了区别于勾股定理的三边的关系,抽丝剥茧发现这种关系是倍角三角形特有的性质,将结论由特殊推广到一般。从而总结出倍角三角形的性质(三边的关系),并举例说明了利用倍角三角形的性质来解决具体问题。这也是一个数学学习者,学习过程中的完整记录。

,





