原题如下:

这是一个关于复数k的连乘。
首先,分析一下k。k是一个复数,是方程x^8-1=0的单位根。表达式中,k的幂次:k,k^2,k^3,...,k^7均位于单位圆上,间隔45°均匀分布:

马上可以知道,当m n=8时,k^m与k^n关于实轴x轴对称,互为共轭。也就是:

这是一个重大发现!想想高斯小朋友计算1 2 3 ... 100=?的清奇思路,首尾相加等于常数101,这里首尾相乘会出现常数1,心潮澎湃的你马上就知道解题的第一步应该怎么搞了:
令

中括号里面复数虚部抵消,这样每一项都是实数,然而,问题似乎并没有变简单,还是七个式子连乘,怎么破?
这条路看起来时走不通了。换个思路。
分析一下表达式。表达式看起来像什么?什么式子中会出现连乘的表达呢?因式分解!!!如果能找到被因式分解的原表达式,而这个表达式计算起来又非常简单,那这个问题也就解决了。
不妨一试。
注意到k是x^8-1=0的根,这是一个8次方程,在复数域上应该有8个根。显然

所以k,k^2,k^3,...,k^7都是方程x^8-1=0的根。别忘了还有一个x=1(有人问,x=-1显然也是根啊,怎么没有?怎么没有,在这儿:k^4=-1)
回忆一元二次方程基于根的因式分解,类似地,有下面的恒等式:

左边,一个极其简单的表达式,右边,一个非常复杂的连乘形式。(插个题外话,上面的因式分解很有内涵,Kummer据此创建了理想数理论,直接证明了费马大定理x^n y^n=z^n无正整数解,对一大批n都成立)。
和原题比较一下,胜利在望~
令x=-3,得

右边,提取8个(-1)以去掉负号,立得
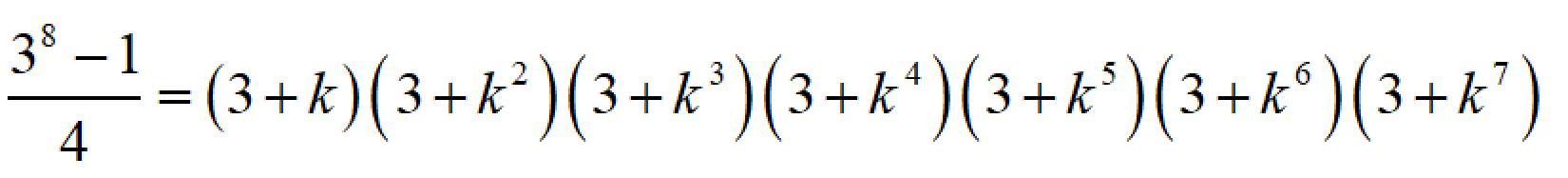
柳暗花明又一村。
老美的数学竞赛还是蛮简单的,加上原题其实是选择题,选项本身就是一种提示,能让你从第一个思路的死胡同里飞出来。难怪听朋友说,他参加州竞赛,拿前三的基本都是亚裔黄种人。
,




