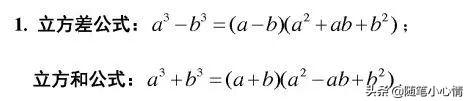这是一道1984年的高考数学题,这届高考数学是史上最难的一次考题。当时全国的平均分30分,北京市的分数,更是人均只有17分,当年的那场考试,一名县城考生考了65分竟然是他本县的第一名,而满分120。
原题如下:
六.(本题满分16分)
1.设p≠0,实系数一元二次方程z2-2pz q=0有两个虚数根z1,z2. 再设z1,z2在复平面的对应点是Z1, Z2. 求以Z1, Z2为焦点且经过圆点的椭圆的长轴的长。
2.求经过定点M(1,2),以y轴为准线,离心率为的椭圆的左顶点的轨迹方程。
解:1. 因为p, q为实数,z有虚解,所以判别式(-2p)2-4q<0, q>p2>0.
根据实系数一元二次方程的求根公式可得:

因为z1,z2为共轭虚数,所以Z1, Z2关于x轴对称,所以椭圆的短轴在x轴上。又由椭圆经过原点,可知原点为椭圆的一个端点。下面是个示意图。
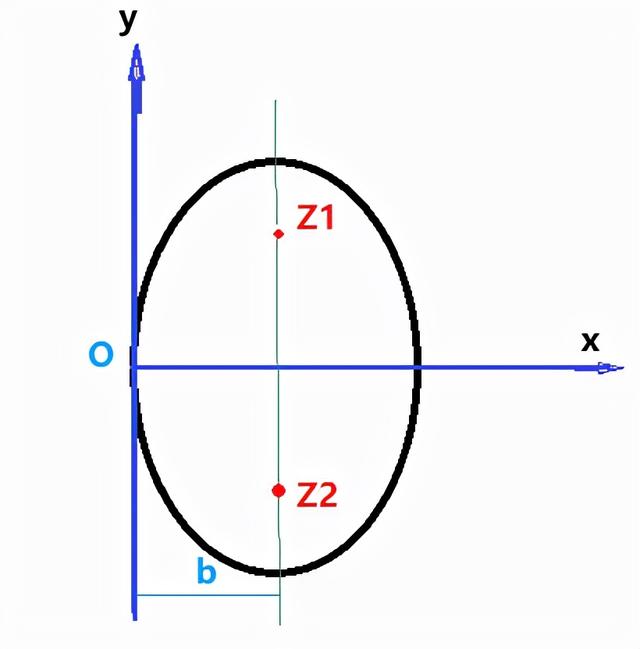
帮助理解的椭圆位置示意图
根据椭圆的性质和复数的几何意义,可知椭圆的短轴长为2b=2︱p︱, 焦距2c=2
所以a2=b2 c2=p2 q-p2=q,
因此长轴长:

2.因为椭圆经过点M(1,2),且以y轴为准线,所以椭圆在y轴右侧,长轴平行于x轴。
可以画个示意图帮助理解:

符合已知条件的一个椭圆示意图
设所求椭圆的左顶点坐标为A(x ,y),因为离心率为1/2,根据椭圆上的点到焦点与到准线的距离关系可知顶点到焦点的距离是顶点到y轴距离的1/2.因而焦点的坐标为F(3x/2,y).
由于M点到准线即y轴的距离为1,所以M点到焦点F的距离为1/2,.
根据这一关系得:定点M到焦点F的距离=定点M到准线的一半距离,列式:

化简得:

这就是所求的轨迹方程。它是一个长轴平行于y轴的椭圆。
PS:总结一下,这道题用到了我前一篇文章中谈到的椭圆很多性质,从定义到特性,从准线到离心率,从焦点到顶点各个基本量的关系。基本定值必须清楚,椭圆的两个定义必须扎实才能顺利解决这道题。
,