本文主要是介绍柯西中值定理推导x→a时0/0型的洛必达法则的思路。
柯西中值定理:
如果函数f(x)及F(x)满足
(1)在闭区间[a,b]上连续;
(2)在开区间(a,b)内可导;
(3)对任一x∈(a,b),F'(x)≠0,
那么在(a,b)内至少有一点 ε( a<ε<b),使等式
[f(b)-f(a)]/[F(b)-F(a)]=f'(ε)/F'(ε)
成立。
x→a时,0/0型的洛必达法则:
设
(1)当x→a时,函数f(x)及F(x)都趋于0;
(2)在点a的某去心邻域内f'(x)及F'(x)都存在且F'(x)≠0;
(3)x→a时 f'(x)/F'(x)的极限存在(或为无穷大),
那么
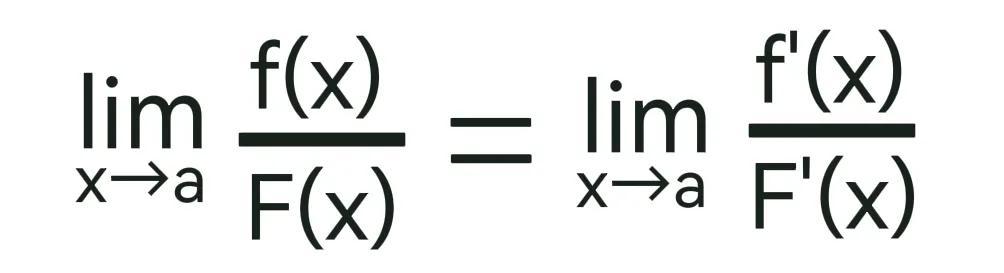
柯西中值定理推导上述型式的洛必达法则思路如下:
由于 f(x)/F(x)在x→a时的极限与f(x)和F(x)在x=a处的值无关。我们可以假定f(a)=F(a)=0,再结合上述洛必法则里的条件(1)和条件(2)可知,f(x)和F(x)在a的某一邻域内是连续的。设x是这一邻域内的一点,那么在以x和a为端点的区间上f(x)和F(x)满足柯西中值定理的3个条件,因此有
[f(x)-f(a)]/[F(x)-F(a)]=f'(ε)/F'(ε)
即f(x)/F(x)=f'(ε)/F'(ε) (式1) 成立,
其中ε介于x与a之间。当x→a时对式(1)等号两端求极限,由于x→a时,ε→a,再根据上述洛必达法则里的条件(3)便得到了想要证明的结论。
以上内容均为个人理解,如有错误,欢迎指正。
,




