Dijkstra算法(迪杰斯特拉算法)是很有代表性的最短路径算法,用于计算一个结点到其他结点的最短路径。该算法指定一个点(源点)到其余各个结点的最短路径,因此也叫做单源最短路径算法。该算法是由荷兰计算机科学家Edsger W.Dijkstra于1959年发表。
Dijkstra算法是一种用于计算带权有向图中单源最短路径算法,不存在回溯的过程,因此它还不适用于带有负权重的情况。如果权值存在负数,那么被派生出来的可能是更短的路径,这就需要过程可以回溯,之前的路径需要被更短的路径替换掉,而Dijkstra算法是不能回溯的,它的每一步都是以当前最优选择为前提的。
Dijkstra算法的思想是广度优先搜索(BFS) 贪心策略。对于计算非加权图中的最短路径,也可使用BFS算法。Dijkstra算法是对BFS算法的推广,以起始点为中心向外层层扩展,并且每一次都选择最优的结点进行扩展,直到扩展到终点为止。Dijkstra算法可以划归为贪心算法,下一条路径都是由当前更短的路径派生出来的更长的路径。
Dijkstra算法在很多专业课程中都作为基本内容有详细的介绍,如数据结构、图论、运筹学等。
二、演示例子例子1第1步,创建距离表。第1列是结点名称,第2列是从起点A到对应结点的已知最短距离。开始我们并不知道A到其它结点的最短距离是多少,默认初始距离是无穷大。如图2-1-1所示:

图2-1-1
第2步,遍历起点A的所有相邻结点,找到起点A的邻接结点B和C。从A到B的距离是5,从A到C的距离是2,刷新距离表中起点A到各结点的最短距离(绿色表示刷新)。如图2-1-2所示。

图2-1-2
第3步,从图2-1-2距离表中找到从A出发距离最短的点,也就是结点C(最小距离是2)。遍历结点C的所有相邻结点,找到结点C的相邻结点D和F(A已经遍历过,不需要考虑)。从C到D的距离是1,所以A到D的距离是A-C-D=2 1=3;从C到F的距离是8;从A到F的距离是A-C-F=2 8=10。然后刷新距离表(绿色表示刷新)。如图2-1-3所示:

图2-1-3
第4步,从图2-1-3距离表中找到从A出发距离最短的点(红色结点C已经遍历过,不需要考虑),也就是结点D(最小距离是3)。遍历结点D的所有相邻结点,找到相邻结点B、E和F(C已遍历过,不考虑)。从A-C-D-B的距离是3 1=4;从A-C-D-E的距离是3 1=4;从A-C-D-F的距离是3 2=5。刷新距离表中起点A到各结点的最短距离。如图2-1-4所示。

图2-1-4
第5步,从图2-1-4距离表中找到从A出发距离最短的点(红色结点C、D已经遍历过,不需要考虑),也就是结点B和E(最小距离是4)。遍历结点B的所有相邻结点,找到相邻结点E(D遍历过,不考虑),从A-C-D-B-E的距离为10,比当前A到E的最小距离4要大,不考虑。遍历结点E的所有相邻结点,找到相邻结点G、B(D遍历过,不考虑),从A-C-D-E-G的距离为4 7=11<∞, 刷新距离表;A-C-D-E-B的距离4 6=10>4,不考虑。如图2-1-5所示。

图2-1-5
第6步,从图2-1-5距离表中找到从A出发距离最短的点(红色结点B、C、D、E已经遍历过,不需要考虑),也就是结点F(最小距离是5)。从A-C-D-F-G的距离为8, 比当前最小距离11要小,刷新距离表。如图2-1-6所示。

图2-1-6
就这样,除终点以外的全部结点都已经遍历完毕,距离表中存储的是从起点A到所有结点的最短距离。
例子2图2-2-1是原始连通图。
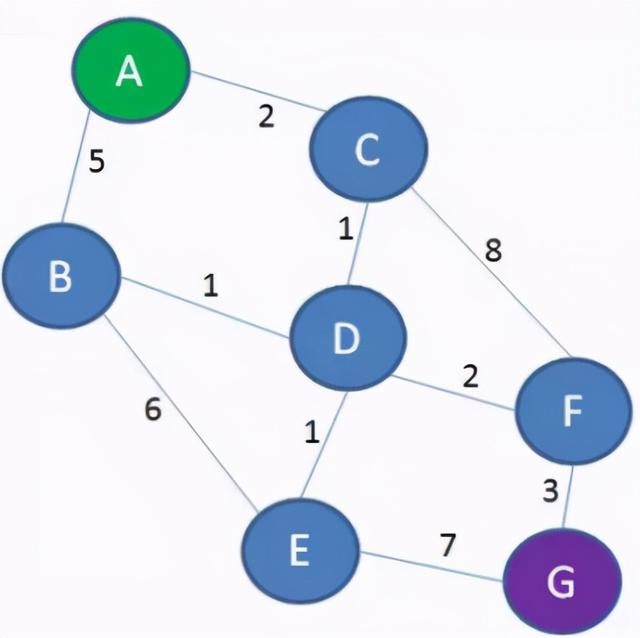
图2-2-1
用Dijkstra算法找出以A为起点的单源最短路径步骤如下:
|
步骤 |
集合S |
集合Q |
|
1 |
选择A到集合S={A} 图2-3-1 三、应用一切能抽象成图或树的场景,如果要求最短路径,Dijkstra算法可考虑。比如,查找两个城市之间的最短路径;在地图中寻找两个地点之间的最短路径;在网络连接中为路由器寻找最短的传输路径等。 ,最新推荐 |





