第二讲 实数的基本性质2
- 实数的阿基米德性:
对于∀a,b属于R ,∃ n属于N,使得nb>a。
理由如下:
设a=a0.a1a2……an……,a0=k属于N,则a<=k 1<10^(k 1).
设b=b0.b1b2……bn……,bp为第一个不为零的正整数,令n=10^(p k 1),则nb>=10^(k 1)>a.
- 实数的稠密性:
1.任意两个不相等的实数a与b之间,必有另一个实数c。
2.任意两个不相等的实数a与b之间,既有有理数又有无理数。
- 实数与数轴上的点一一对应。
1.对于这种对应关系,粗略的可描述为:
设p是数轴上的一点(不妨设在0的右边),若p在整数n与n 1之间,则a0=n。
把(n,n 1)十等分,若点p在第i个区间,则a1=i。
类似可得到an,n=2,3……,这时,令点p对应于a0.a1a2…an…
反之,任何一实数也对应于数轴上一点。
2.实数集与数轴上点的一一对应关系反映了实数的完备性。
- 实数的绝对值与三角不等式:
1.实数a的绝对值|a|定义为:
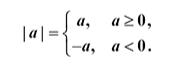
2.实数的绝对值性质:
(1)|a|=|-a|>=0;当且仅当a=0时,|a|=0
(2)-|a|<=a<=|a|;
(3)|a|<h等价于-h<a<h,|a|<=h等价于-h<=a<=h。
(4)|a|-|b|<=|a b|<=|a| |b|(三角形不等式)。
(5)|ab|=|a||b|
(6)|a/b|=|a|/|b|(b不等于0)
3.三角形不等式|a|-|b|<=|a b|<=|a| |b|的证明:






