欧拉公式推导和差公式 欧拉公式对哈密顿四元数的推广

欧拉公式指欧拉关于复数的公式：

相信大家非常熟悉，而对Hamilton四元数可能就比较陌生了。

这里先简要介绍一下。

Hamilton四元数

Hamilton四元数是一种超复数，由英国数学家Hamilton发明。复数是由实数加上虚数单位i 组成，其中i^2 = -1。 类似地，四元数都是由实数加上三个虚数单位 i、j、k 组成，一般可记为

a表示q的标量部分，v=bi cj dk，表示q的向量部分。所以简单地说，四元数就是”1维实数 3维向量“的组合。

四元数的运算

四元数本身很好理解，稍微麻烦一点的是关于q的二元运算，包括加法和乘法两种运算。加法和通常意义上的加法一样。因为在复数i的基础上，又引入了j和k，所以乘法需要考虑这些新元素之间的运算关系。乘法则具有如下规则：

若

则根据前面的运算规则，有

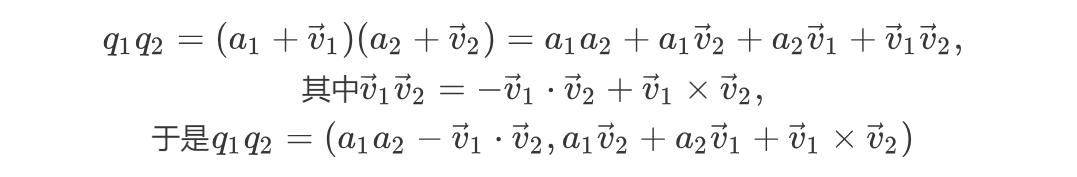
“.“和”ד表示通常意义上的向量的数量积（点乘）和矢量积（叉乘）。很神奇的计算结果，一个运算同时包含了向量的点乘和叉乘。

特别地，若a=0,则

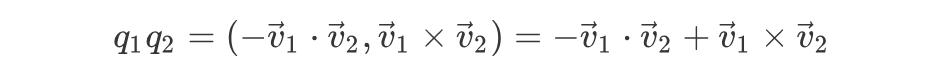
容易知道，该乘法运算满足结合律但不满足交换律。

当四元数q的向量部分只有一个分量时（bi cj dk，b,c,d中有两个数等于0），四元数退化成通常意义上的复数，满足复数的所有运算性质。

举个运算的例子：

广义欧拉公式

现在，我们来讨论欧拉公式在四元数上地推广，也就是：

看到这样一个指数表达式，该如何下手呢？

一切函数都是多项式。考虑指数函数的泰勒展开：

表达式是关于q的幂次。先考虑简单的情形，a=0，即q只包含向量部分。于是

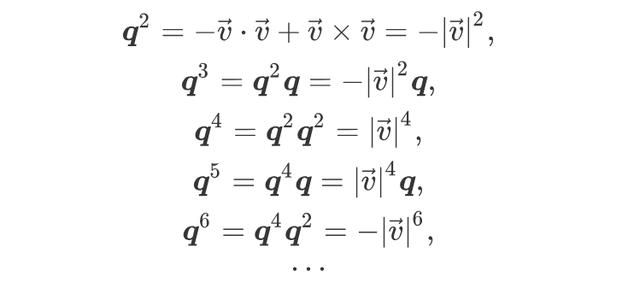
从而

对比欧拉公式

两者的相似性显而易见。当q只包含一个向量分量时，关于四元数的欧拉公式就退化成了经典的欧拉公式。

最后，讨论一下当a≠0的情形。容易验证，标量和任何四元数都满足乘法交换律和结合律。

从而

也就是欧拉公式在四元数上最一般的形式。

,