题目:
如图,E是中点,阴影部分面积为50,求正方形ABCD的面积
知识点回顾:
正方形性质定理- 两组对边分别平行;四条边都相等;邻边互相垂直。
- 四个角都是90°,内角和为360°。
- 对角线互相垂直;对角线相等且互相平分;每条对角线平分一组对角。
- 既是中心对称图形,又是轴对称图形(有四条对称轴)。
- 正方形的一条对角线把正方形分成两个全等的等腰直角三角形,对角线与边的夹角是45°;正方形的两条对角线把正方形分成四个全等的等腰直角三角形。
- 正方形具有平行四边形、菱形、矩形的一切性质与特性。
- 正方形是特殊的矩形,正方形是特殊的菱形。
粉丝解法1:
S△EMD=1/2×S△CMD=1/2×S△BMES△EMD=10S□=4×30=120
粉丝解法2:
s△CMD=s△BME=2s△EMD,5s△EMD=50,s△EMD=10,∴1/2CDx1/2CD=30,CD^2=s正=120。
粉丝解法3:
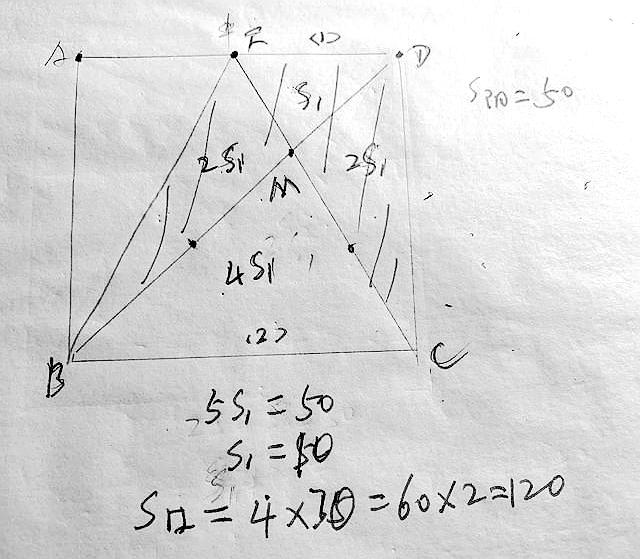
粉丝解法4:
edm:bcm:emb:dmc=1:4:2:2阴影部分:1 2 2的面积是50则edc=30正方形面积:30*4=120
粉丝解法5:
△1与△4相似ED/BC=1/2设S△1为a则S△4为4a 则(50-a/2)²=4a² 两段开方(50-a/2)=2a 解a=10S△4=40 S△2=S△3=20S△5=10 20=30S□=30 20 20 10 40=120

粉丝解法6:
s梯BCDE=(3/4)sABCDs△BCM=BCx(2/3)CD/2=sABCD/3sBCDE-s△BCM=50,即是(3/4-1/3)sABCD=50sABCD=50x12/5=120
粉丝解法7:
∵ED:BC=1/2:1=1:2,∴ED边上的高=1x1/(1 2)=1/3,∴正方形ABCD面积:50÷(1-1/4x2-1/2x1/3x1/2)=50÷5/12=120
粉丝解法8:
解:由图据可得,E是AD中点,M是BD的三份点,即,阴影部分可分为5等,正方形ABCD可分12等分。则正方形面积=50÷5X12=120。
粉丝解法9:

粉丝解法10:
设正方形的边长为a,ME:MC=s△BDE:s△BCD=1/4:1/2=1:2,s△DEM=1/3s△CDE=1/3x1/4×a^2=a^2/12,s阴=(2x1/4-1/12)a^2=5a^2/12=50,sABCD=a^2=120。
,