一、恒成立有解问题
例题1、设函数 f(x)= lnx , g(x)= ax (a - 1)/ x - 3 (a ∈ R)。
(1)当 a = 2 时 , 解关于 x 的方程 g(e^x)= 0 (其中 e 为自然对数的底数);
(2)求函数 ψ(x)= f(x) g(x)的单调区间 ;
(3)当 a = 1 时 , 记 h(x)= f(x)· g(x),是否存在整数 λ ,使得关于 x 的不等式 2λ ≥ h(x)有解?
若存在 ,请求出 λ 的最小值 ;若不存在,请说明理由 。(参考数据:ln2 ≈ 0.6931,ln3 ≈ 1.0986)
解:

例题1图(1)
故所求的方程的根为 x = 0 , 或 x = -ln2 。
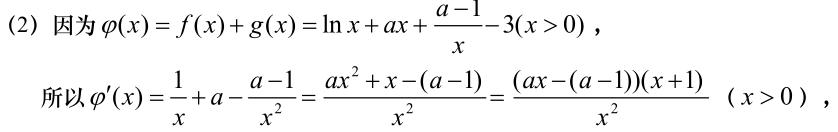
例题1图(2)
① 当 a = 0 时 ,由 ψ'(x)> 0 , 解得 x > 0 ;
② 当 a > 1 时 ,由 ψ'(x)> 0 , 解得 x > (a-1)/a ;
③ 当 0 < a < 1 时,由 ψ'(x)> 0 , 解得 x > 0 ;
④ 当 a = 1 时,由 ψ'(x)> 0 , 解得 x > 0 ;
⑤ 当 a < 0 时 ,由 ψ'(x)> 0 , 解得 0 < x < (a-1)/ a 。
综上所述:
当 a < 0 时 ,ψ(x)的增区间为 (0,(a-1)/ a);
当 0 ≤ a ≤ 1 时,ψ(x)的增区间为 (0, ∞);
当 a > 1 时 ,ψ(x)的增区间为 ((a-1)/ a, ∞)。
(3)当 a = 1 时 ,g(x)= x - 3 , h(x)= (x - 3)lnx ,
所以 h'(x)= lnx 1 - 3/x 单调递增 , h'(3/2)= ln(3/2) 1 - 2 < 0 , h'(2)= ln2 1 - 3/2 > 0 ,
所以存在唯一 x0 ∈ (3/2 , 2)使得 h'(x0)= 0 ,即 lnx0 1 - 3/(x0) = 0 ,
当 x ∈ (0 , x0)时,h'(x)< 0 , 当 x ∈ (x0 , ∞)时,h'(x)> 0 ,
所以

例题1图(3)
记函数 r(x)= 6 - ( x 9/x ) , 则 r(x)在 (3/2 , 2)上单调递增 ,
所以 r(3/2)< h(x0)< r(2), 即 h(x0)∈(-3/2 , -1/2),
由 2λ ≥ -3/2 ,且 λ 为整数 , 得 λ ≥ 0 ,
所以存在整数 λ 满足题意 , 且 λ 的最小值为 0 。
注:本题旨在考查解一元二次方程,利用导数研究函数的性质(单调性和最值),不等式恒成立问题,构造函数,运用函数的思想求解,考查运算和推理能力,难度较大 。
二、零点问题
例题2、已知函数 f(x)= ax^2 - x - lnx , a∈ R 。
(1)当 a = 3/8 时 , 求函数 f(x)的最小值 ;
(2)若 -1 ≤ a ≤ 0 , 证明 :函数 f(x)有且只有一个零点 ;
解:
(1)当 a = 3/8 时 ,f(x)= ( 3/8) x^2 - x - lnx , 所以

例题2图(1)
令 f '(x)= 0 , 得 x = 2 ,
当 x∈(0 , 2)时 , f '(x)< 0 ;当 x∈(2 , ∞)时 , f '(x)> 0 ,
所以函数 f(x)在 (0 , 2)上单调递减,在 (2 , ∞) 上单调递增 。
所以当 x = 2 时 ,f(x)有最小值 f(2)= -1/2 - ln2 。
(2)

例题2图(2)
函数 f(x)在 (0 , ∞)上单调递减 ,
所以当 a ≤ 0 时 ,函数 f(x)在 (0, ∞)上最多有一个零点 。

例题2图(3)
所以当 -1 ≤ a ≤ 0 时 , 函数 f(x)在 (0, ∞)上有零点 。
综上 , 当 -1 ≤ a ≤ 0 时 ,函数 f(x)有且只有一个零点 。
,




