我们都知道行测考试中的数量关系难度普遍较高,尤其是排列组合问题,因为它考查类型多样、灵活性强,所以一直是很多考生避之不及的痛点。但事实上,排列组合中也有一些考法相对固定、容易拿分的经典模型,这些模型特征明显、解法固定且容易上手,是不可错过的香饽饽。今天就带大家一起来认识一下其中的一种经典模型:环形排列。
模型介绍“n个人围成一个圆圈,问一共有多少种不同的方法。”从模型可以看出,在安排人的过程中,元素是以环形的形式、首尾相连进行排列的,所以称作环形排列问题。
例题分析例15个小朋友围成一圈做游戏,请问有多少种位置安排?
A.120 B.24 C.12 D.6
错误思路:5个小朋友围成一圈,因为人和人是不一样的,在进行位置安排时导致结果不一样,所以列式为
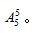
思路点拨:根据上面的思路,我们把这5个小朋友用A、B、C、D、E分别展示出来,观察一下5种座位方式有无区别?具体如图1所示。很显然,本质是一样的,5个人的相对位顺序都没有变。

图1顺时针排列
【答案】B。解析:从上图可以发现,虽然每个人的实际位置发生了变化,但每个人的“相对位置”没有发生变化,即左右两侧的人是不变的,因此我们认为这5种情况属于同一种排法,每一种情况被重复计算了5次。因此计算结果应为

除此之外,我们也可以理解为一个人的位置固定之后,其他人的相对位置才能确定,那么从结果上来看,就相当于计算4个小朋友的相对位置排列,可以直接列式为
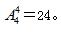
因此选择B项。
结论:n个不同的人环形排列时方法数为

将红、黄、蓝、绿四种颜色的四个珠子串成手环,共有几种串法?
A.3 B.6 C.12 D.24
错误思路:本题可以理解为4颗珠子以环形的形式排列,符合环形排列问题特征。所以可列式为

思路点拨:根据上面的思路,我们把这4颗珠子的位置分别展示出来,观察一下2种串法有无区别呢?具体如图2所示。很显然,对于手环来讲,左图和右图只是同一个手环的正反两面,所以左、右两种排列方式本质上是同一个手环,是没有区别的。

【答案】A。解析:对于一个手环而言,从正面观察,顺时针排列颜色为红-黄-绿-蓝;翻面观察,逆时针排列颜色也为红-蓝-绿-黄,因此实际上还是属于同一种情况,这就意味着对同一种情况重复计算了2遍。所以计算结果应为

选择A项。
结论:n个不同颜色的珠子串成手环(项链)等的环形排列时,需额外注意翻面导致的重复,方法数应为

通过以上题目的练习,相信大家知道如何解决“环形排列”的问题了,希望能够快快动起手来,通过练习提升自己的熟练度吧!
,




