熵:熵是一个随机变量不确定性的度量。对于一个离散型变量,定义为:

一个随机性变量的熵越大,就表示不确定性越大,也就是说随机变量包含的信息量越大。
熵只依赖于X的分布,与X的取值无关。
条件熵:条件熵 H(Y|X) 表示在已知随机变量 X 的条件下随机变量 Y 的不确定性,H(Y|X) 定义为在给定条件 X 下,Y 的条件概率分布的熵对 X 的数学期望:
公式为:

互信息:互信息表示在得知 Y 后,原来信息量减少了多少。

如果X与Y相互独立,则互信息为0。
KL散度(相对熵)与JS散度:KL散度指的是相对熵,KL散度是两个概率分布P和Q差别的非对称性的度量。KL散度越小表示两个分布越接近。也就是说KL散度是不对称的,且KL散度的值是非负数。
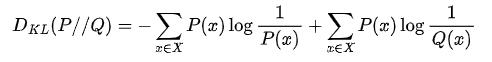
JS散度是基于KL散度的变种,度量了两个概率分布的相似度,解决了KL散度的非对称问题。如果两个分配P,Q离得很远,完全没有重叠的时候,那么KL散度值是没有意义的,而JS散度值是一个常数。这在学习算法中是比较致命的,这就意味这这一点的梯度为0。梯度消失了。
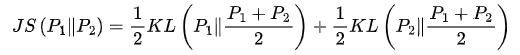
三者关系
【知识图谱实战特训】价值千元课程,金三福利限时1元秒,仅限前150名,先到先得!
https://www.julyedu.com/course/getDetail/410&from=TT
课程结合了理论与实践,尽可能让大家学完后能在工业场景项目中落地。带领大家从图谱的构建开始,学习图谱的存储结构,主流的图数据库,图算法并分别介绍结构化数据与非结构化数据如何构建成图谱。

问题2:机器学习泛化能力评测指标
泛化能力是模型对未知数据的预测能力。
准确率:分类正确的样本占总样本的比例
准确率的缺陷:当正负样本不平衡比例时,当不同类别的样本比例非常不均衡时,占比大的类别往往成为影响准确率的最主要因素。
精确率:分类正确的正样本个数占分类器预测为正样本的样本个数的比例;
召回率:分类正确的正样本个数占实际的正样本个数的比例。
F1 score:是精确率和召回率的调和平均数,综合反应模型分类的性能。
Precision值和Recall值是既矛盾又统一的两个指标,为了提高Precision值,分类器需要尽量在“更有把握”时才把样本预测为正样本,但此时往往会因为过于保 守而漏掉很多“没有把握”的正样本,导致Recall值降低。
ROC曲线的横坐标为假阳性率(False Positive Rate,FPR);纵坐标为真阳性 率(True Positive Rate,TPR)。FPR和TPR的计算方法分别为
精确度(precision)/查准率:TP/(TP FP)=TP/P 预测为真中,实际为正样本的概率
召回率(recall)/查全率:TP/(TP FN) 正样本中,被识别为真的概率
假阳率(False positive rate):FPR = FP/(FP TN) 负样本中,被识别为真的概率
真阳率(True positive rate):TPR = TP/(TP FN) 正样本中,能被识别为真的概率
准确率(accuracy):ACC =(TP TN)/(P N) 所有样本中,能被正确识别的概率
上式中,P是真实的正样本的数量,N是真实的负样本的数量,TP是P个正样本中被分类器预测为正样本的个数,FP是N个负样本中被分类器预测为正样本的个数。
AUC:AUC是ROC曲线下面的面积,AUC可以解读为从所有正例中随机选取一个样本A,再从所有负例中随机选取一个样本B,分类器将A判为正例的概率比将B判为正例的概率大的可能性。AUC反映的是分类器对样本的排序能力。AUC越大,自然排序能力越好,即分类器将越多的正例排在负例之前。
回归问题
RMSE:RMSE经常被用来衡量回归模型的好坏。
RMSE能够很好地反映回归模型预测值与真实值的偏离程度。但在实际问题中,如果存在个别偏离程度非常大的离群点(Outlier)时,即使离群点 数量非常少,也会让RMSE指标变得很差。
MAPE:引入别的评价指标,MAPE,平均绝对百分比误差
相比RMSE,MAPE相当于把每个点的误差进行了归一化,降低了个别离群点带来的绝对误差的影响。
F1-score:在多分类问题中,如果要计算模型的F1-score,则有两种计算方式,分别为微观micro-F1和宏观macro-F1,这两种计算方式在二分类中与F1-score的计算方式一样,所以在二分类问题中,计算micro-F1=macro-F1=F1-score,micro-F1和macro-F1都是多分类F1-score的两种计算方式。
micro-F1:计算方法:先计算所有类别的总的Precision和Recall,然后计算出来的F1值即为micro-F1;
使用场景:在计算公式中考虑到了每个类别的数量,所以适用于数据分布不平衡的情况;但同时因为考虑到数据的数量,所以在数据极度不平衡的情况下,数量较多数量的类会较大的影响到F1的值;
marco-F1:计算方法:将所有类别的Precision和Recall求平均,然后计算F1值作为macro-F1;
使用场景:没有考虑到数据的数量,所以会平等的看待每一类(因为每一类的precision和recall都在0-1之间),会相对受高precision和高recall类的影响较大。
问题3:过拟合和欠拟合过拟合:是指训练误差和测试误差之间的差距太大。换句换说,就是模型复杂度高于实际问题,模型在训练集上表现很好,但在测试集上却表现很差。
欠拟合:模型不能在训练集上获得足够低的误差。换句换说,就是模型复杂度低,模型在训练集上就表现很差,没法学习到数据背后的规律。
如何解决欠拟合?
欠拟合基本上都会发生在训练刚开始的时候,经过不断训练之后欠拟合应该不怎么考虑了。但是如果真的还是存在的话,可以通过增加网络复杂度或者在模型中增加特征,这些都是很好解决欠拟合的方法。
如何防止过拟合?
数据的角度:获取和使用更多的数据(数据集增强);
模型角度:降低模型复杂度、L1\\L2\\Dropout正则化、Early stopping(提前终止)
模型融合的角度:使用bagging等模型融合方法。
问题4:生成式模型和判别式模型生成模型:学习得到联合概率分布P(x,y),即特征x,共同出现的概率
常见的生成模型:朴素贝叶斯模型,混合高斯模型,HMM模型。
判别模型:学习得到条件概率分布P(y|x),即在特征x出现的情况下标记y出现的概率。
常见的判别模型:感知机,决策树,逻辑回归,SVM,CRF等。
问题5:L1和L2区别L1是模型各个参数的绝对值之和。
L2是模型各个参数的平方和的开方值。
L1会趋向于产生少量的特征,而其他的特征都是0。 因为最优的参数值很大概率出现在坐标轴上,这样就会导致某一维的权重为0 ,产生稀疏权重矩阵
L2会选择更多的特征,这些特征都会接近于0。 最优的参数值很小概率出现在坐标轴上,因此每一维的参数都不会是0。当最小化||w||时,就会使每一项趋近于0。
L1的作用是为了矩阵稀疏化。假设的是模型的参数取值满足拉普拉斯分布。
L2的作用是为了使模型更平滑,得到更好的泛化能力。假设的是参数是满足高斯分布。
【知识图谱实战特训】价值千元课程,金三福利限时1元秒,仅限前150名,先到先得!
https://www.julyedu.com/course/getDetail/410&from=TT
课程结合了理论与实践,尽可能让大家学完后能在工业场景项目中落地。带领大家从图谱的构建开始,学习图谱的存储结构,主流的图数据库,图算法并分别介绍结构化数据与非结构化数据如何构建成图谱。






