3.14是圆周率日,也是国际数学日。今天这篇文章主要介绍从古代开始到现代的圆周率竞赛。
我们知道,圆周率是圆的周长与直径之比。神奇的是,不管这个圆是多大,它的周长与直径之比都是一个常数。圆周率π与自然对数的底e是数学里最著名的两个常数。π是一个无理数,同时也是超越数,约等于3.1415926。在日常生活中,通常都用3.14代表圆周率去进行近似计算。数学爱好者们也将3月14日称之为π节。
人类很早就有对圆周率的记载。古巴比伦的一块石匾(约产于公元前1900年至公元前1600年)清楚地记载了圆周率=25/8=3.125。同一时期的古埃及文物——莱因德数学纸草书(Rhind Mathematical Papyrus)——也表明圆周率等于分数16/9的平方,约等于3.1605。埃及人可能在更早时候就知道圆周率了。建于公元前2500年左右的胡夫金字塔的周长和高度之比恰好等于圆周率的两倍,为圆的周长与半径之比,这不应是巧合。中国古代算书《周髀算经》(约公元前2世纪)中有“径一而周三”的记载,意即取π=3。在1500年前,我国南北朝的数学家祖冲之就已经计算出圆周率约等于3.1415926。

那么,人类是怎么能将圆周率计算得那么精确呢?圆周率的计算大概经过了四个时期:实验时期、几何法时期、分析法时期、计算机时期。
实验时期
在古代,人们通过实验对π值进行估算,这是计算π的第一阶段。这种对π值的估算基本上都是以观察或实验为根据,是基于对一个圆的周长和直径的实际测量而得出的。但是,受限于测量的精度,凭直观推测或实物度量来计算π值所得到的结果是相当粗略的。

几何法时期
真正使圆周率计算建立在科学的基础上,首先应归功于古希腊大数学家阿基米德(史上四大数学家之一)。他开创了人类历史上通过理论计算圆周率近似值的先河。阿基米德采用的方法就是“割圆术”,即利用圆的内接和外切正多边形的周长来逼近圆的周长。比如,如果想得到圆周率的下限,那么可以从圆的内接正多边形开始。

下图左为圆的内接正六边形,下图右则为圆的内接正十二边形。可以看到,正十二边形已经比较接近于圆了。如果我们再进一步分割为正24、正48乃至正96边形,那肉眼将慢慢难以分辨所画的图形到底是正多边形还是圆。
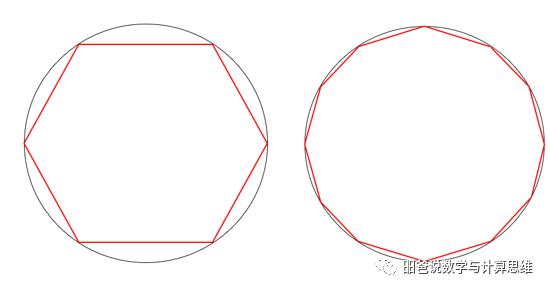
最简单地,在圆的内部构造一个内接正六边形(如下图),圆的周长>6A1A2,而由于△OA1A2为正三角形,所以圆周长2πr>6r,故π>3,即3为圆周率的一个下界。

反之,如果在圆的外部构造一个外切正六边形(如下图所示),则有:
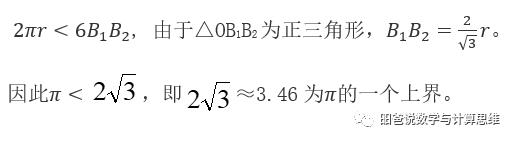

古代的圆周率竞赛基本就是沿用阿基米德的方法。到公元150年左右,希腊天文学家托勒密得出π=3.1416的结果,取得了自阿基米德以来的巨大进步。我国魏晋时期的数学家刘徽就是遵循“割之弥细,所失弥少,割之又割以至于不可割,则与圆合体而无所失矣”的思想,一直分割到了内接1536边形,得到了3.1416的结果。我国南北朝时期的数学家祖冲之首次将“圆周率”精确计算到小数点后第七位,即在3.1415926和3.1415927之间,这一结果领先了欧洲近千年。

在国外,1150年,印度数学家婆什迦罗第二计算出圆周率的值π=3927/1250=3.1416。1424年,中亚细亚地区的天文学家、数学家卡西第一次打破祖冲之的记录,他计算了3×228=805,306,368边内接与外切正多边形的周长,将圆周率小数点后的准确数字扩充至十七位,求得π=3.14159265358979325。
16世纪的法国数学家韦达利用阿基米德的方法计算π近似值,用正6×216边形,推算出精确到9位小数的π值。17世纪初,德国人鲁道夫用了几乎一生的时间钻研这个问题,但他不是从正六边形开始并将其边数翻番的,而是从正方形开始的。1610年,正值古稀的鲁道夫终于计算出262边形的周长,成功地将π值计算到了35位,这一数值为:3.1415926535 89793 23846 26433 83279 50288。鲁道夫为此颇感自豪,自知身体大限将至的他当即留下遗言,让后人把这个π值铭刻在他的墓碑上。为了记念他的这一非凡成果,在德国圆周率π被称为“鲁道夫数”。

但是,用几何方法求π值,计算量很大,这样算下去,穷数学家一生也改进不了多少,到鲁道夫可以说已经登峰造极。想要在计算π的道路上再向前推进,必须在方法上有所突破。
数学分析法时期
17世纪出现了数学分析,这一锐利的工具使得许多初等数学束手无策的问题迎刃而解。π的计算历史也随之进入了一个新的阶段。数学家们发现了若干个数学级数,如果实施无穷多次运算,就能精确计算出π小数点后面的多位数字。显然,级数方法宣告了古典方法的过时。自此,对于圆周率的计算像马拉松式竞赛,纪录一个接着一个地诞生。下面是基于数学分析法人工计算π值的里程碑。

人们常用于计算π值的几个级数如下:
- 格雷戈里 - 莱布尼茨无穷级数
1671年,格雷戈里发现:

将x=1代入就得到了计算π/4的公式:
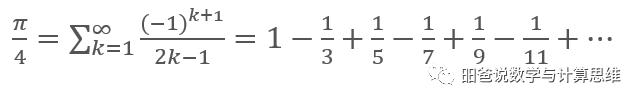
将两边乘以4,就得到了圆周率π的值。这是一个最有名和最简单的用于计算π的无穷级数。每一次迭代,结果都会更接近π的精确值。但是,这个算法的最大问题是效率比较低,为了得到小数点后两位精确度,需要迭代300次才行,而为了得到小数点后10位精确度,需要迭代 500000次!
由于上面的方法收敛速度比较慢,一种改进方法是使用下面的无穷级数,最后乘以6即可。

1706年,John Machin得到了下面的公式,收敛速度更快:

- 沃利斯公式(Wallis formula)
沃利斯公式是圆周率π的有理数极限表达式,它是第一个把无理数π/2表示成容易计算的有理数列的极限的重要公式,在理论上很有意义。这个公式在1655年就被提出,早于格雷戈里 - 莱布尼茨公式。
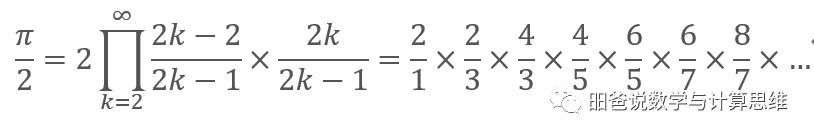
- 尼拉坎塔(Nilakantha) 级数
这是可用于计算π的另一个无穷级数,非常容易理解。在该公式中,从3开始,依次交递加减以4为分子、三个连续整数乘积为分母的分数,每次迭代时三个连续整数中的最小整数是上次迭代时三个整数中的最大整数。反复计算几次,结果与π非常接近,相比于格雷戈里 - 莱布尼茨公式,这个公式收敛速度更快。

计算机时代
在计算机出现之前,计算π的难度相当大。英国人尚克斯在1873年的时候将π值计算到了707位,他自认无人可比,以此为荣,在死后将这一结果也刻在了墓碑上。悲哀的是,到了1945年,他的一位英国老乡弗格森证明了从528位之后,数值就是错误的。但这一结果,尚克斯已无从得知,所以有人说,他的最不幸的,也是最幸运的。
不过,在计算机被发明后,历史上几千年来人工计算出的圆周率都成为了小儿科。计算机的出现使得圆周率的精度以几何级数在提升。下表给出了2000年以前计算机上计算的圆周率结果。可以看到,在人类发明的第一台计算机ENIAC上,就计算出了小数点后2037位的圆周率精度,远超人类手工计算的结果。

计算机能够快速地计算圆周率,一方面得益于高精度算术操作高效算法的发现,例如快速傅里叶变换(FFT)可以比传统的方法更快速地执行高精度的乘法,另一方面也得益于计算π值的更高效和更低复杂度算法的发现。比如,Gosper在1985年用印度数学家拉马努金发明的公式把π值计算到了17000000位。
- 拉马努金(Ramanujan) 公式
拉马努金的圆周率公式能够以非常少的迭代步数快速计算出π的近似值。这个公式看上去很古怪,但用计算机计算起来并不复杂。

上世纪的1976年,EugeneSalamin和Richard Brent独立发现了计算π值的低复杂度算法。它基于算术几何平均迭代以及高斯在1800年左右的一些思想。通过这种迭代,每一次都可以把圆周率的精度翻倍,25次迭代就可以得到4500万的精度。但这种方法最大的问题是大规模傅里叶变换对内存和并行系统节点之间通信带宽的要求极高。因此,虽然基于arctan的级数展开的方法时间复杂度较高,但由于空间和通信复杂度较低,依然是不错的选择。
2019年3月14日,谷歌宣布圆周率已到小数点后31.4万亿位。2021年8月5日,由瑞士科研人员通过一台超级计算机耗时108天零9个小时计算出来的圆周率数值已精确到了小数点后62.8万亿位。如果把这个最新的π印成书,按每一位一个字算,那么总字数是四库全书总字数的6万多倍!如果每本书按100万字计算的话,那么一共可以印6280万册书,几乎是中国国家图书馆藏书量的两倍!
作者:昍爸,中科院计算机博士,大学计算机专业教授,曾获初中和高中全国数学奥林匹克联赛一等奖,江苏赛区第一名,高考数学满分。著有《给孩子的数学思维课》与《给孩子的数学解题思维课》
,




