一、知识点梳理
1、平面向量的坐标表示:
在直角坐标系中,分别取与 x 轴、y 轴方向相同的两个单位向量

作为基底,由平面向量的基本定理知,该平面内的任一向量
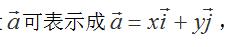
由于 α 与数对(x,y) 是一一对应的,因此把 (x,y) 叫做向量 α 的坐标,记作 α =(x,y),其中 x 叫作 α 在 x 轴上的坐标,y 叫做在 y 轴上的坐标 。
(1) 相等的向量坐标相同,坐标相同的向量是相等的向量 ;
(2) 向量的坐标与表示该向量的有向线段的始点、终点的具体位置无关,只与其相对位置有关 。
2、平面向量的坐标运算:

3、两个向量的数量积:
已知两个非零向量

它们的夹角为 θ ,

4、向量的投影:

5、数量积的几何意义:

6、向量的模与平方的关系:

7、两个向量的数量积的坐标运算:

8、向量的夹角:
已知两个非零向量



9、垂直:

10、两个非零向量垂直的充要条件:

二、考点突破
1、向量的坐标运算
例1、如图,在 △ABC中,AD=DB,AE=EC,CD 与 BE 交于 F,




2、向量共线的条件
例题2、(1)已知向量a=(sinx,1),b=(cosx,-3),且a∥b,则tanx=________.



3、平面向量的基本定理
例题3、


(2)如图,在△ABC中,D、E 分别是 BC、AC 的中点,F 为 AB上一点,



(3) 在△ABC中,过中线 AD 的中点 E 任作一条直线分别交 AB、AC 于M、N 两点,



4、向量的数量积
例题4、



[解析] 以 AB 所在的直线为 x 轴,AB 的垂直平分线为 y 轴,建立如图所示的平面直角坐标系,


5、向量的模
例5、设角A,B,C 是 △ABC 的三个内角,已知向量m=(sinA+sinC,sinB-sinA),n=(sinA-sinC,sinB),且m⊥n。
(1)求角 C 的大小;
(2)若向量 s =(0,-1) ,

试求 |s+t| 的取值范围。
解析:


6、向量的夹角
例6、(1) 设非零向量a,b,c 满足|a|=|b|=|c|,a+b=c,则a,b的夹角为
A.150° B.120° C.60° D.30°
(2) 若向量 a、b 满足 |a|=|b|=1,(a+b)·b=3/2 ,则向量 a、b 的夹角为
A.30° B.45° C.60° D.90°


7、两向量平行与垂直的充要条件
例7、
(1) 在△ABC中,a、b、c分别是∠A,∠B,∠C所对的边,设向量m=(b-c,c-a),n=(b,c+a),若m⊥n,则∠A的大小为?









