如果对本文存在有疑问或需要工具可以在下方给我留言!
文中涉及的工具有IDA,yafu
文中涉及的算法有RSA
这题比较简单。
题目下载地址:https://www.lanzous.com/iawzl2f
程序没有加壳,直接IDA载入

直接分析main函数,我们可以看到程序的逻辑很清晰。使用GDB调试得知sub_96A函数是把用户输入的字符串转换为16进制存入v9中。继续往下看,程序调用了 __gmpz_init_set_str 函数,通过搜索得知这是一个 GNU 高精度算法库,官方文档地址:https://gmplib.org/manual/
__gmpz_init_set_str 其实就是 mpz_init_set_str
int mpz_init_set_str (mpz_t rop, const char *str, int base) [Function]
Initialize rop and set its value like mpz_set_str
int mpz_set_str (mpz_t rop, const char *str, int base) [Function]
Set the value of rop from str, a null-terminated C string in base base. White space is allowed
in the string, and is simply ignored.
这三个参数分别是多精度整数变量,字符串,进制。这个函数的作用就是将 str 字符数组以 base 指定的进制解读成数值并写入 rop 所指向的内存。然后后面还调用了一个__gmpz_powm函数,官方文档中的定义是这样。
void mpz_powm (mpz_t rop, const mpz_t base, const mpz_t exp, const mpz_t mod) [Function]
Set rop to base^exp mod mod.
其实就是计算 base 的 exp 次方,并对 mod 取模,最后将结果写入 rop 中这个运算的过程和RSA的加密过程一样。接下来就是__gmpz_cmp函数,看这个函数名就知道这是比较函数。
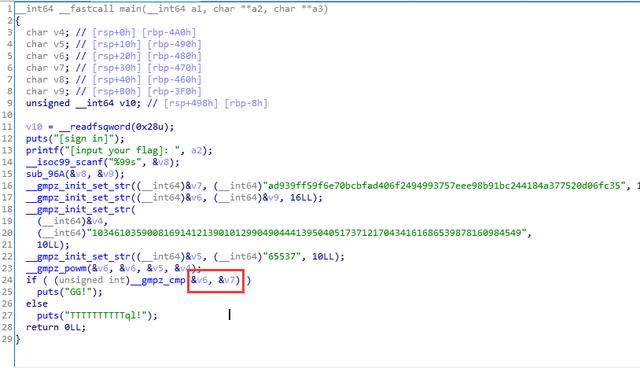
v6是用户输入,v7是程序的硬编码数据接下来我们简单了解下RSA的加解密算法,只要简单理解一下RSA算法,就可以做出这题。加密算法:

图中的C是密文,M是明文,E是公钥(E和 φ(N)互为质数),N是公共模数(质数 P 、Q相乘得到N),MOD就是模运算解密算法:

图中的C是密文,M是明文,D是私钥(私钥由这个公式计算得出E * D % φ(N) = 1),N是公共模数(质数 P 、Q相乘得到N),MOD就是模运算,φ(N)是欧拉函数(由这个公式计算得出φ(N) = (P-1)(Q-1))。
了解了加密解密的概念,我们就可以开始写脚本来解密了通过分析程序的这个函数

可以得知以下信息
C = 0xad939ff59f6e70bcbfad406f2494993757eee98b91bc244184a377520d06fc35
N = 103461035900816914121390101299049044413950405173712170434161686539878160984549
E = 65537
知道这3条数据我们就可以开始解密密文了,首先我们要分解N得到P、Q,这里我使用 yafu 工具。下载地址:https://nchc.dl.sourceforge.net/project/yafu/1.34/yafu-1.34.zip
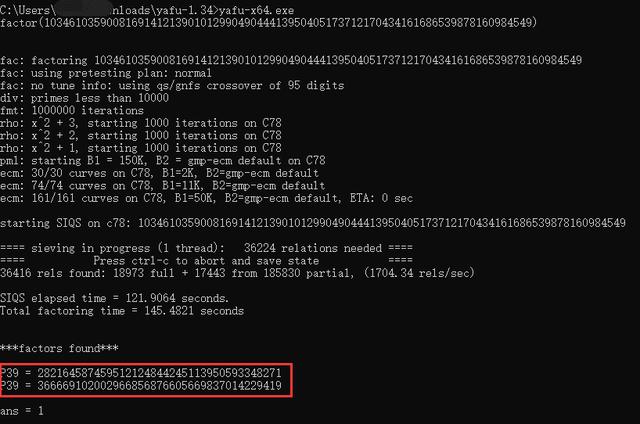
成功得到P、Q
P = 282164587459512124844245113950593348271
Q = 366669102002966856876605669837014229419
现在我们有了P、Q和E,我们就可以计算出欧拉函数,然后我们就可以通过欧拉函数φ(N)和公钥E计算出私钥D。使用python的gmpy2库计算私钥。(E * D % φ(N) = 1)
d = gmpy2.invert(e,(p-1)*(q-1))
d = 91646299298871237857836940212608056141193465208586711901499120163393577626813
计算出私钥d后我们就可以对密文C进行解密,解密算法是(密文C的私钥D次方对公共模数N取余)使用python的gmpy2库计算明文
m = gmpy2.powmod(c,d,n)
得到
m = 185534734614696481020381637136165435809958101675798337848243069
把m转为字符串即可!解密脚本
import gmpy2
import binascii
p = 282164587459512124844245113950593348271
q = 366669102002966856876605669837014229419
c = 0xad939ff59f6e70bcbfad406f2494993757eee98b91bc244184a377520d06fc35
n = 103461035900816914121390101299049044413950405173712170434161686539878160984549
e = 65537
d = gmpy2.invert(e,(p-1)*(q-1))
m = gmpy2.powmod(c,d,n)
print(binascii.unhexlify(hex(m)[2:]).decode(encoding="utf-8"))
suctf{Pwn_@_hundred_years}
成功拿到flag

验证结果,可以看到程序输出Tql(太强了),这题属于逆向中比较简单的题目了,本文主要为了记录自己所学知识,与大家分析,共同进步,同时也希望大家可以指出文中不足之处。
,




