作函数图像的一般步骤:1、求函数的定义域;2、考察函数的奇偶性、周期性;3、求函数的某些特殊点,如与两个坐标轴的交点,不连续点,不可导点等;4、确定函数的单调区间,极值点,凸性区间以及拐点;5、考察渐近线;6、画出函数图象。
练习:按函数作图的一般步骤,作f(x)=xe^(-x)的图像.
请动手画一画这个函数的图像。
分析:函数在R上可导,不存在奇偶性和周期性。因为f(0)=0,所以函数的曲线过原点。
求函数的一阶导数:f'(x)=e^(-x)-xe^(-x)=(1-x)e^(-x). 当f'(x)=0时,x=1. 也就是说函数有唯一的稳定点x=1. 下面分析函数在稳定点两侧的单调性。
当x<1时,f'(x)>0,原函数单调递增;当x>1时,f'(x)<0,原函数单调减。函数在x=1两侧,左增右减,说明(1,e^(-1))是函数的极大值点。由于函数在R上可导,所以并不存在其它极值点。
继续求二阶导数,以判断函数的凸性区间,并找到可能存在的拐点。
f"(x)=-e^(-x)-(1-x)e^(-x)=(x-2)e^(-x). 当x<2时,f"(x)<0,曲线在这个区间上是上凸的;当x>2时,f"(x)>0,曲线在这个区间上是下凸的,也就是凹的。
函数在点x=2两侧凸性不同,且在这一点连续,因此点(2,2e^(-2))是函数的拐点。
观察发现, 函数并不存在竖直的渐近线。那就设函数有斜的渐近线y=ax b,由求渐近线参数的极限公式,有:
a=lim(x->∞)(f(x)/x)=lim(x->∞)e^(-x)=0. 这说明,函数有一条水平的渐近线。注意,当a=0时,函数就有一条水平的渐近线。但我们求的时候,还是把它当作斜的渐近线去求的。其实竖直渐近线也可以用这种方法求得的。
b=lim(x->∞)(f(x)-ax)=lim(x->∞)xe^(-x)=0. 所以函数有一条水平的渐近线y=0.

综上,函数的图像性态可以概括如下表:
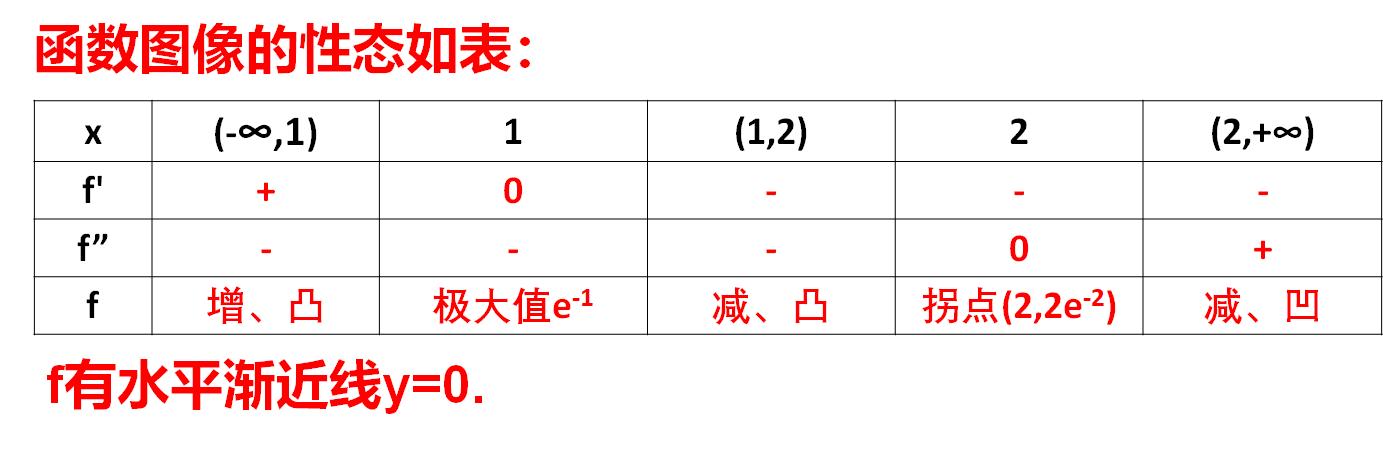
可以看到,函数有两个关键点,极大值点x=1和拐点x=2, 将函数的定义域划分成三个区间。最左边的区间上,函数上凸且单调递增;在中间的区间上,函数上凸且单调递减;在右边的区间上,函数下凸且单调递增。不要忘了曲线还过原点。
综合这所有的信息,结合函数的渐近线,作得函数的图像如下图:

和你所做的图像是否一样呢?
,




