在公务员行测考试中,极值问题考查频率比较高,并且其题目特征明显,题目难度中偏下,因此,广大考生任需对该类题目有所了解。今天,就带着大家一起来看看极值问题中的“一元二次函数求极值”问题如何利用“中点法”快速求解。
一、一元二次函数基本定义一般地,把形如
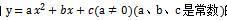
的函数叫做二次函数,其中a称为二次项系数,b为一次项系数,c为常数项。x为自变量,y为因变量。
二、函数性质一元二次函数的图像是开口向上或开口向下的抛物线,且抛物线是轴对称图形。故函数在对称轴的顶点

处取得最大值(a<0)或最小值(a>0),且对称轴在x轴上的坐标点(

【例1】某商店出售A商品,若每天卖100件,则每件可获利6元。根据经验,若A商品每件涨1元钱,每天就少卖10件。为使每天获利最大化,A商品应涨价:
A.6元 B.4元 C.2元 D.10元
【中公解析】C。设A商品每天获利最大化应涨价x元。由题分析,根据“


处取得最大值,每天获利最大,故选C。
【例2】某类商品按质量分为8个档次,最低档次商品每件可获利8元,每提高一个档次,则每件商品的利润增加2元。最低档次商品每天可产出60件,每提高一个档次,则日产量减少5件。若生产其中某一档次的商品,则每天能获得的最大利润是( )元。
A.620 B.630 C.640 D.650
【中公解析】C。设该商品生产的档次为x,由题分析,根据“

”建立等量关系,有

解得:

取最大值,最大利润

,故选C。
由以上两个例题不难看出,利用“中点法”求二次函数的最大值或最小值,核心就在于找到对称轴在x轴上的坐标点x,即抛物线与x轴的两个交点——

,方程的两个根

最后,广大考生可加强对此类基础题型、简单题型的梳理和练习,争取在考试中拿下它们!加油!
,