我们在一元微积分中对如下的微分算子都很熟悉:和,差,积,商的微分公式

我们现在重新引入此符号的原因是我们不仅要接受与变量X有关的导数,还需要其它更多变量的导数,所以需要一些明确的符号来区分哪个变量

现在假设我们有一个同时依赖于X和Y的函数,我们将其称为f(x,y),这最终将称为曲面而不是曲线

那么这个曲面的变化率是多少,我们要做的就是找到它的变化率,如果想要找到X的变化率,我们仅将Y作为常数,以此区分作为变量的X,我们使用弯曲的D代替常规的D,这称之为偏导数

同样,如果我们想要Y方向的变换量,这将是关于y的偏导数,在这种情况下,我们会将X视作常数

如下是一个示例:关于X和Y的偏导数
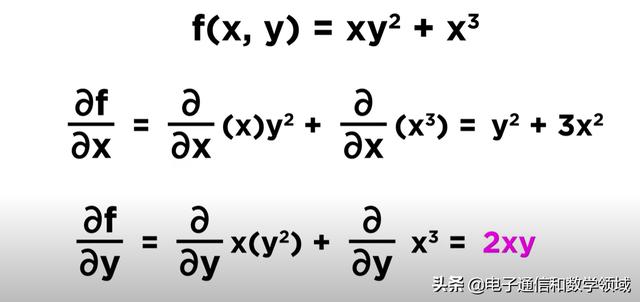
现在,我们将介绍一个结合了这些偏导数,即所谓的梯度,函数的梯度只是一个向量,它有所有的偏导数组成

我们可以写成gradf
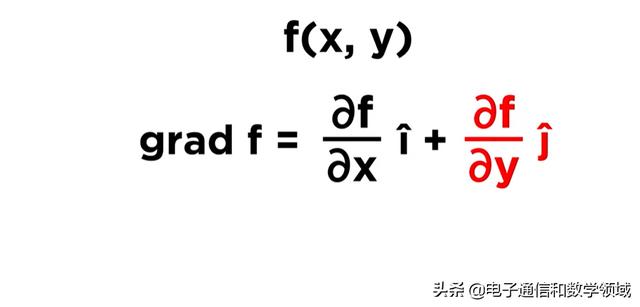
如果在三个维度上,梯度就是

这个向量它指向函数最大变化的方向,并等于最大变化率的幅度

这个有关向量的偏导数,即梯度用倒置的三角形表示,称为del







