中考数学几何压轴题折叠题（中考数学提分36计之第20计）

在几何的解题中，当题目给出的条件显得不够或者不明显时，我们可以将图形作一定的变换，这样将有利于发现问题的隐含条件，抓住问题的关键和实质，使问题得以突破，找到满意的解答．图形变换是一种重要的思想方法，它是一种以变化的、运动的观点来处理孤立的、离散的问题的思想，很好地领会这种解题的思想实质，并能准确合理地使用，在解题中会收到奇效，也将有效地提高思维品质．

初中图形变换主要包含翻折、平移和旋转，我们要通过实验、操作、观察和想象的方法掌握运动的本质，在图形的运动中找到不变量，然后解决问题。

中考数学几何压轴题折叠题（中考数学提分36计之第20计）(1)

一、利用对称变换解决问题

通过作关于某一直线或一点的对称图，把图形中的图形对称到另一个位置上，使分散的条件集中在一起.当出现以下几种情况时，经常考虑用此变换：

（1）轴对称、中心对称条件；（2）垂线条件；（3）图形折叠问题.

翻折（轴对称）变换：把一个图形变为关于某一直线为对称轴的轴对称图形，这种变换称为轴对称变换，在几何图形中，如果是轴对称图形，则常添置对称轴，以充分利用对称性质，如果遇到不是轴对称图形，则常选择某条直线为轴，补添为轴对称图形；或将轴一侧的图形通过翻折反射到另一侧，以实现条件的相对集中；

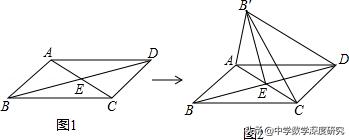
1．（2019春•邗江区期中）如图，▱ABCD中，对角线AC与BD相交于点E，∠AEB＝45°，BD＝2，将△ABC沿AC所在直线翻折180°到其原来所在的同一平面内，若点B的落点记为B′，则DB′的长为（）

A．1B．√2C．3/2D．√3

中考数学几何压轴题折叠题（中考数学提分36计之第20计）(2)

【解析】本题主要考查了折叠的对称性以及平行四边形的性质，解决折叠问题的关键是找到对应相等的边和角，构造新的三角形求解．

∵四边形ABCD是平行四边形，∴BE＝1/2BD＝1．

连接BB′，由折叠性质可知：∠AEB＝∠AEB＝45°，BE＝B′E．

∴∠BEB′＝90°．∴△B′BE是等腰直角三角形．∴BB′＝√2BE＝√2．

又∵BE＝DE，B′E⊥BD，∴DB′＝BB′＝√2．故选：B．

2．（2019春•洪泽区期中）如图，在正方形ABCD中，△ABE是等边三角形，点E在正方形ABCD内，在对角线AC上有一点P，若PD PE的最小值为5，则正方形的面积为（）

A．16 B．6.25 C．9 D．25

中考数学几何压轴题折叠题（中考数学提分36计之第20计）(3)

【解析】此题主要考查了最短路线问题，难点主要是确定点P的位置．注意充分运用正方形的性质：正方形的对角线互相垂直平分．再根据对称性确定点P的位置即可．要灵活运用对称性解决此类问题．设BE与AC的交点为点P．如图，连接PD，则此时PD PE的和最小．∵四边形ABCD是正方形，∴点D与点B关于AC对称，∴PD PE＝PB PE＝BE＝5．

又∵△ABE是等边三角形，∴AB＝BE＝5．∴正方形的面积为25，故选：D．

3．（2019•婺城区模拟）如图，正方形ABCD的边长为（√2 1），点M、N分别是边BC、AC上的动点，沿MN所在直线折叠正方形，使点C的对应点C'始终落在边AB上，若△NAC'为直角三角形，则CN的长为_____ ．

中考数学几何压轴题折叠题（中考数学提分36计之第20计）(4)

【解析】由正方形的性质可得AC＝√2×（√2 1）＝2 √2，AB＝√2 1，∠CAB＝45°，分∠NC'A＝90°和∠C'NA＝90°两种情况讨论，若∠C'NA＝90°，

∴∠AC'N＝∠CAB＝45°∴AN＝NC'，

∵由折叠性质，∴CN＝C'N，∴CN＝AN＝1/2AC＝(2 √2)/2,

若∠NC'A＝90°∴∠ANC'＝∠CAB＝45°,∴NC'＝AC',∴AN＝√2AC'＝√2C'N

∵由折叠性质，∴CN＝C'N,∵AC＝CN AN＝√2CN CN＝2 √2,∴CN＝√2

故答案为：√2或(2 √2)/2

点评：折叠前后的图形关于折痕成轴对称.解决这类问题的关键首先要把握折叠的变换规律，弄清折叠前后哪些量变了，哪些量没有变，又有哪些条件可利用；其次要充分挖掘图形的几何性质，利用等腰三角形、全等三角形、勾股定理或相似三角形的知识，将其中的数量关系用方程的形式表达出来，由此解决问题.

中考数学几何压轴题折叠题（中考数学提分36计之第20计）(5)

二、利用平移变换解决问题

把图形中的某一个线段或者一个角移动到一个新的位置，使图形中分散的条件紧密地结合到一起.

平移有2种方法：（1）平移已知条件，（2）平移所求问题，把所求问题转化，其实就是逆向证明.图形变换题多数是逆向思考的.

平移变换：是指在平面内，将一个图形上的所有点都按照某个方向作相同距离的移动，这样的图形变换叫做平移变换，简称平移。平移不改变图形的形状和大小。图形经过平移，对应线段相等，对应角相等，对应点所连的线段相等。当题设中有彼此平行的线段或构成平行的某种因素，又需要将有关线段或角集中到一块的时候，常常考虑平移变换。

4．（2019春•鹿城区校级月考）如图，将边长为12cm的正方形纸片ABCD沿其对角线AC剪开，再把△ABC沿着AD方向平移，得到△A′B′C′，若两个三角形重叠部分（见图中阴影）的面积为32cm2，则它移动的距离AA′等于（）

A．6cmB．8cmC．6cm或8cmD．4cm或8cm

中考数学几何压轴题折叠题（中考数学提分36计之第20计）(6)

【解析】本题考查了平移的性质．解决本题关键是抓住平移后图形的特点，利用方程方法解题．设AC交A′B′于H，

∵∠A＝45°，∠D＝90°，∴△A′HA是等腰直角三角形

设AA′＝x，则阴影部分的底长为x，高A′D＝12﹣x

∴x•（12﹣x）＝32，解得x ₁＝4，x ₂＝8，

即AA′＝4cm或AA′＝8cm，故选：D．

5（2019春•武胜县期中）如图，在平面直角坐标系中，点A，B的坐标分别为（﹣1，0），（3，0），现同时将点A，B分别向上平移2个单位，再向右平移1个单位，分别得到点A，B的对应点C，D，连接AC，BD．在y轴上存在一点P，连接PA，PB，使S△PAB＝S四边形ABDC．则点P的坐标为_______ ．

中考数学几何压轴题折叠题（中考数学提分36计之第20计）(7)

【解答】由平移可得，C（0，2），D（4，2），∴CD＝AB＝4，CD∥AB，

∴四边形ABCD为平行四边形，∴四边形ABCD面积＝4×2＝8，

又∵S△PAB＝S四边形ABDC，∴△PAB的面积为8，即1/2×AB×OP＝8，∴OP＝4，

∴当点P在AB下方时，P（0，﹣4）；当点P在AB上方时，P（0，4），

故答案为：（0，﹣4）或（0，4）．

6．（2019•石景山区一模）如图，在等边△ABC中，D为边AC的延长线上一点（CD＜AC），平移线段BC，使点C移动到点D，得到线段ED，M为ED的中点，过点M作ED的垂线，交BC于点F，交AC于点G．

（1）依题意补全图形；

（2）求证：AG＝CD；

（3）连接DF并延长交AB于点H，用等式表示线段AH与CG的数量关系，并证明．

中考数学几何压轴题折叠题（中考数学提分36计之第20计）(8)

【分析】本题考查平移变换、等边三角形的性质、三角形全等的性质和判定、平行四边形的判定和性质等知识，解题的关键灵活应用所学知识解决问题，正确作出辅助线构造全等三角形是解题的关键，属于中考常考题型．

【解答】（1）补全的图形如图1所示．

（2）证明：∵△ABC是等边三角形，

∴AB＝BC＝CA．∠ABC＝∠BCA＝∠CAB＝60°．

由平移可知ED∥BC，ED＝BC．∴∠ADE＝∠ACB＝60°．

∵∠GMD＝90°，如图1，∴DG＝2DM＝DE．

∵DE＝BC＝AC，∴DG＝AC．∴AG＝CD．

中考数学几何压轴题折叠题（中考数学提分36计之第20计）(9)

（3）线段AH与CG的数量关系：AH＝CG．

证明：如图2，连接BE，EF．

∵ED＝BC，ED∥BC，∴四边形BEDC是平行四边形．

∴BE＝CD，∠CBE＝∠ADE＝∠ABC．

∵GM垂直平分ED，∴EF＝DF．∴∠DEF＝∠EDF．

∵ED∥BC，∴∠BFE＝∠DEF，∠BFH＝∠EDF．∴∠BFE＝∠BFH．

∵BF＝BF，∴△BEF≌△BHF（ASA）．∴BE＝BH＝CD＝AG．

∵AB＝AC，∴AH＝CG．

【方法总结】利用平移解决问题，首先确定平移方向和距离.平移前后图形全等，只是位置发生了变化；采用转化数学思想，图形上所有点的平移是一致的；平移结合轴对称图形.

中考数学几何压轴题折叠题（中考数学提分36计之第20计）(10)

三、利用旋转变换解决问题

几何图形的旋转变化是近年来中考中的考点多与三角形四边形相结合解决旋转变化问题要明确旋转中心旋转方向和旋转角关键是找不旋转前后的对应点旋转前后图形全等性质解题

把一个图形绕一个定点（旋转中心）按一定的方向、一个角度旋转而得到另一个图形，这种变换称为旋转变换，旋转中心、旋转方向和旋转角度为旋转变换的三要素，特殊地，当旋转角度为1800时，称为中心对称变换。中心对称的代表图形是平行四边形系列，旋转变换的作用也是将相关元素和条件相对集中，为充分运用已知条件提供方便。

7．（2019•增城区一模）如图，点P为等边△ABC内一点，若PC＝3，PB＝4，PA＝5，则∠BPC的度数是______ ．

中考数学几何压轴题折叠题（中考数学提分36计之第20计）(11)