本篇文章从微信群的讨论开始,最后由詹大师的总结结束。
话说:上次詹大师发表了一篇“逗比”系列第二波:逗比的SPC“真相”。文章一经发出,引起了热烈的讨论。此时,有学员在制造学习联盟的微信群里发问了:
如果数据不正态。怎么办?
接下来让我们来看看群里的大师们,如何做精彩的交锋讨论。

潘*:

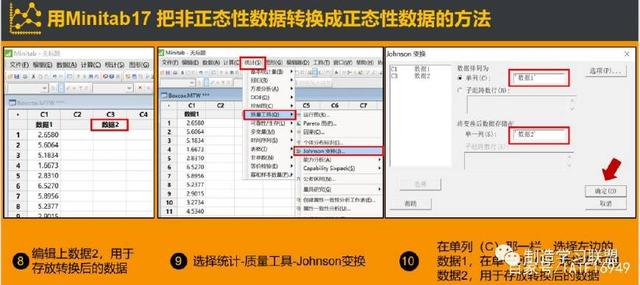
詹大师:
我来总结一下,如果数据不正态应该怎么办?
首先,从逻辑上来讲,我们通常讲的Cpk(过程能力指数),在计算这个指标之前,需要满足四大前提,MSA、独立性、稳定性、正态性。MSA我们将会在后续课程里面详细介绍,独立性会在黑带课程里面介绍,那么我们现在先假定,测量系统的MSA满足要求,同时数据抽样是随机的(在机械制造行业里,这样可以认为满足独立性)。
剩下的是稳定性和正态性,稳定性是由常规控制图来监控的,如果常规控制图没有发现判异,那么我们认为过程稳定性没有异常。
最后就是正态性,某些老师认为直方图可以作为正态性的检验方法,这本身没错,但是要记得直方图是定性的检验方法,如果客户要你定量检验,那就需要用“逗比(二)”的方法才分析,如果通过,那就可以计算Cpk了,如果不通过,先看看是不是分辨率的问题,“逗比(二)”就完整的介绍了这个问题的解决方法。
如果数据确实不正态,那么即使控制图没有判异,也不能硬套公式来计算Cpk,很多人会奇怪,数据不正态为什么控制图不判异,这里面涉及中心极限定理的概念,我们后续再介绍。
那么,数据应不应该正态呢?要看数据形成的机理。
通常,在机械行业里,如果这个尺寸是一维的,那么数据的机理就可以认为应该是正态的,比如长度、宽度、高度等,这些尺寸只在一个维度(坐标上)考量,直径的话,如果我们用两点测量法,也可以认为是近似在一个维度产生的。
但是,对于GD&T里面的那些行位公差,现在官方叫法应该是“几何公差”,就要仔细考量了,它们的数据形成机理就不一定是正态的,最有代表性的是“位置度”
位置度是多维的尺寸,可以是二维(平面)的,或是三维(空间)的,具体的维度,要看图纸的标注,现在我们假设是二维的吧,它的计算方法是,测量得到被侧中心x坐标和零点的偏移Δx,以及被测中心y坐标和零点的偏移Δy
位置度=2*SQRT(Δx^2 Δy^2),其中,SQRT是开根号的意思,^2是平方的意思,本质上Δx和Δy的机理都是正态分布的,正态分布有一个特性,它的线性函数还是正态分布,什么叫线性函数,就是 和-,然后在有就是乘以一个常数,比如L=2x 3y,这就是线性函数,如果x和y都是正态分布(当然要满足独立性),那么L也是正态分布
但是我们再回过头来看位置度的公式,位置度=2*SQRT(Δx^2 Δy^2),很明显这不是线性函数,又有平方又有开根号,所以,位置度的数据,本身的数据形成机理就不是正态的
所以,在计算Cpk的时候,如果发现数据不正态,不可以“不管三七二十一”先进行变换,而是要分析数据的形成机理(主要是从数据的维度方面考虑),如果机理不正态,那么转换或者寻找其它分布来拟合是合适的,否则,就应该去调查数据为什么不正态
,




