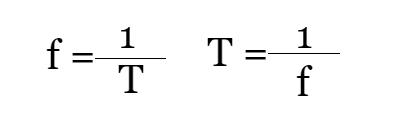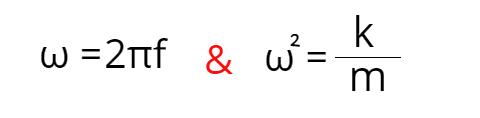前几期的文章我们介绍了颜色的奥秘、彩虹的物理学原理以及彩虹的颜色,感兴趣的朋友可以戳下面链接:一口气搞懂︱双彩虹,霓虹,微笑彩虹和月虹背后的物理学原理
下面的几期文章我们将详细介绍声音的物理学原理,在这之前我们将用两篇文章描述振动、简谐运动物理学和波的物理学。
我们首先要了解的是:振动是宇宙中普遍存在的现象,大到所有的宏观物体(地震),小到基本粒子(热运动、布朗运动)。
振动(又称振荡)是指一个状态改变的过程。即物体的往复运动。在高中物理,可以定量研究(可以用公式法、作图法、列表法给出确定数值)的只有四种最简单的运动:匀变速直线运动、匀速圆周运动、抛体运动和简谐振动。
当一个物体发生振动时,物体会从平衡位置来回移动。如果一个物体静止不动,位置不发生任何变化,这时我们说这个物体上受到的净力为零。所以,当我们给一个物体施加一个外力时,物体的平衡状态会被打破,物体开始远离平衡点,要么发生匀速直线运动,要么发生振动运动,物体在某一点后停止,然后回到平衡点,紧接着移动到另一边,然后停止,然后再回来,如此往复运动……
振动在我们在日常生活中随处可见。从我们车里的摇头娃娃、家里的摆钟、掉在地板上弹球、秋千上的孩子、在风中摇摆的树,或任何其他摇动和摇摆的动作,通常这些物体要么富有弹性,或者是一个像钟摆一样的物体。但是如果我们深入的研究,我们会发现,所有的东西都在振动,即使是看起来静止的固体。在固体中,粒子也在振动,只有在绝对零度(-273℃)时,所有运动将会停止。我们今天主要讨论的是宏观物理学的振动和周期运动。
周期运动
当物体的振动表现出规律和往复运动时,我们称这种运动为周期性运动。物体在同一时间内沿着同一路径往复运动,直到阻尼停止。弹簧上的配重是学习周期运动最好的例子,看上图:
在上面的动画中,我们先把配重拉到最低点也就是起始的位置,然后松手,从最低位置开始,配重会上升到平衡点,并经过平衡点,继续上升,直到停止,这就完成了周期运动的一半;然后配重会在弹簧的恢复力和重力作用下改变方向,开始返回,在返回的过程中,配重会再次经过平衡点,并回到底部最低点。所有的过程我们称之为一个循环,总共由4个部分组成。
配重完成一个循环的时间叫做周期。
由于运动的过程是以秒为单位度量的,所以周期的单位也是秒,我们用大写字母T来表示。如果我们把这个定义反过来问:在一段时间内发生了多少个周期的运动?那么我们就有了另外一个衡量周期运动的物理量:频率。频率用f表示,单位为赫兹(Hz)。周期与频率的关系如下:
周期和频率存在直接的联系。周期是完成一个完整的循环运动所需要的时间,频率是单位时间内完成的周期数。如果我们知道其中一个物理量就很容易得到另外一个。
在周期运动中还会经常提到的另一个定义:振幅。上文中的弹簧配重的最大位移,这就是振幅。用大写字母A表示,单位为米(m)。
振幅是一个物体离开平衡位置的最大位移。
简谐振子(运动)关于弹簧,上文已经讲了一些基本的常识,现在介绍一下简谐运动。
弹簧的一端连接一个重物,而另一端连接到一个刚性支架上。当系统静止在平衡位置时,作用在重物上的合力为零。质量从平衡位置发生位移时,弹簧会产生一种使整个系统恢复平衡的弹力,这就是我们熟知的胡克定律。
胡克定律说明了拉伸或压缩弹簧所需的力(F)与发生的位移X成线性关系。弹簧的弹力总是跟配重运动方向和位移X的方向相反,因为当弹簧被压缩时,弹力把整个系统往下推,当弹簧被拉长时,弹力会把整个系统往回拉,弹力趋向于使系统恢复平衡。这就是公式F =- kx有个负号的原因。
在公式中F(单位为牛顿)为恢复力(弹力),x为位移(单位为米),k为弹性系数,该常数取决于弹簧的材料。
我们来看看整个运动过程:
当我们把一个重物挂在弹簧上,系统处于静止,这时重物处于平衡位置,合力为零。因为弹簧的力等于把物体拉向地面的力。这时我们从平衡位置将重物移开然后松手,重物会受到弹簧所产生的净恢复力,重物会向平衡位置移动。越接近平衡位置,恢复力就越小,直到在平衡位置降为零,这时加速度为零。在我们刚松手时,加速度最大,这就是简谐运动的起点。
在重物到达平衡时,由于动能的原因,弹簧会被压缩,重物继续向上运动。当弹簧压缩时,向下的加速度增加,恢复力使重物减速,直到重物在振幅处停止,此时向下的加速度再次达到最大值,重物开始下降,而加速度也再次下降,直到再次达到平衡位置时降为零。当重物经过平衡位置时,开始减速,直到到达开始时的底部振幅。
如果整个过程中没有能量损失,运动就会一直重复,我们就有了一个简谐振子。由于阻尼会造成能量损耗,振幅会随着时间的推移越来越小,直到最后为零,运动也将停止。
一个做匀速圆周运动的物体在一条直径上的投影所做的运动即为简谐运动。
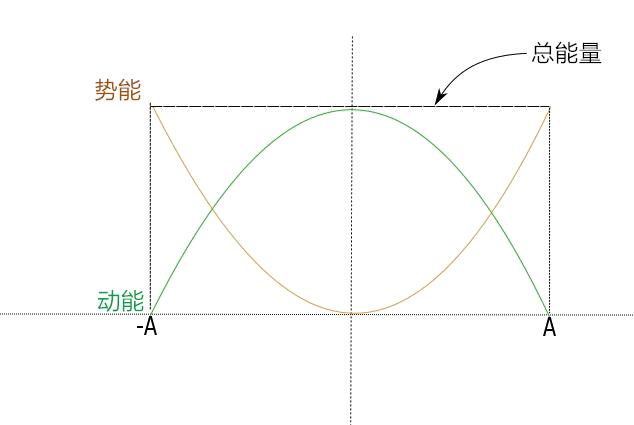
这个过程中的能量变化是怎么样的我们首先要知道的是,一个物体静止时有势能,有速度时有动能,我们就能很容易地理解这个运动过程中的能量变化。我们来看下图:
总能量是动能和弹性势能的和。我们从振幅的最低位置开始,物体是静止的。因为此时速度为零,所以没有动能,整个能量是势能。当物体开始运动时,势能减小,而动能随着速度的增加而增加。在平衡状态时,势能为零,整个能量为动能。当物体继续上移到振幅较高的位置时,动能减小,势能增加,直到上升到振幅的位置,动能为零,整个能量都是势能。
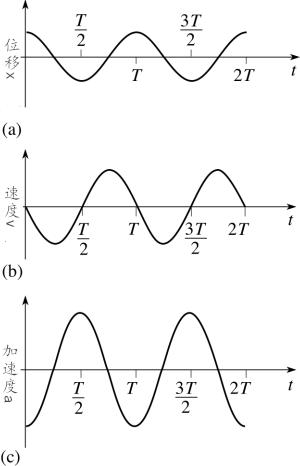
我们发现,位移、速度和加速度都具有周期性。我们可以解微分方程得到三角函数解。
上图都是微分方程的解和角频率ω= 2πf。
从下图中可以看出,位移从振幅开始,速度从0开始,加速度从最大值开始。函数是周期性变化的。
现在我们来看一个关于周期和频率的重要问题。也就是周期和频率的决定因素是什么?如果我们改变质量,运动会改变吗?如果我们有相同的质量,但增加振幅,运动会改变吗?
周期和频率与振幅无关
不管你把重物向下拉几厘米还是几米,周期和频率都是一样的。我们来看看为什么会这样。我们知道,角频率是ω= 2πf,我们也知道角动量取决于质量和弹簧常数,如以下公式所示:
我们现在要做的就是把这两个公式结合起来,看看会得到什么。
总结
就像我们一开始说的,为了得到声音,我们首先需要讨论波,讨论波之前,我们需要了解振动。上文我们已经讲述了振动以及从位移、加速度到能量和频率的简谐运动。下篇文章我们就说一下波的物理学。
,