
2017年中考刚结束,很多中考生总算可以暂时扔下厚重的书本,可以好好放松一下。不过,对于另外一部分特殊的学生群体,中考气氛却越来越紧张。初二的学生马上面临期末考试,更重要是下半年直升初三。毫不夸张的说,这些“准初三”学生随着2017年中考一结束,他们的2018年中考“战争”就打响了。
2018年中考会考什么?要考什么?所有家长、学生和老师都非常关心,但大家永远要记住一点,具体题目是没法猜测,唯一能做的就是努力自己,学好自己,以不变应万变。就像刚参加完2017年中考的考生,他们在过去整整一年中考复习冲刺,只有不断冲刺,不断努力,拒绝投机取巧,才能真正战胜中考。
因此,对于2018年中考生来说,只好踏踏实实去努力学习,掌握好每一个知识点,吃透数学思想方法,学会用知识去解决具体实际问题,才能在中考“大浪”中脱颖而出。接下去本人会不断推出一些跟中考相关文章,希望考生们能细细阅读,认真对待。借用一位读者话来说,如果一年下去,能把本人所写的题目都去吃透,其实面对中考数学问题是不大。
几何相关类型问题一直都是中考数学的热点,中考数学常考题型,在中考数学中仍占有相当的比例,这主要是基于几何知识能很好体现数学逻辑关系,考查考生思维能力。今天我们就一起来讲讲中考数学热点问题,几何中跟四边形相关的知识内容。
一、四边形的相关知识概念
1、四边形
在同一平面内,由不在同一直线上的四条线段首尾顺次相接的图形叫做四边形。
2、凸四边形
把四边形的任一边向两方延长,如果其他个边都在延长所得直线的同一旁,这样的四边形叫做凸四边形。
3、对角线
在四边形中,连接不相邻两个顶点的线段叫做四边形的对角线。
4、四边形的不稳定性
三角形的三边如果确定后,它的形状、大小就确定了,这是三角形的稳定性。但是四边形的四边确定后,它的形状不能确定,这就是四边形所具有的不稳定性,它在生产、生活方面有着广泛的应用。

二、平行四边形相关知识概念
1、平行四边形的概念
两组对边分别平行的四边形叫做平行四边形。
平行四边形用符号“□ABCD”表示,如平行四边形ABCD记作“□ABCD”,读作“平行四边形ABCD”。
2、平行四边形的性质
(1)平行四边形的邻角互补,对角相等。
(2)平行四边形的对边平行且相等。
推论:夹在两条平行线间的平行线段相等。
(3)平行四边形的对角线互相平分。
(4)若一直线过平行四边形两对角线的交点,则这条直线被一组对边截下的线段以对角线的交点为中点,并且这两条直线二等分此平行四边形的面积。

3、平行四边形的判定
(1)定义:两组对边分别平行的四边形是平行四边形
(2)定理1:两组对角分别相等的四边形是平行四边形
(3)定理2:两组对边分别相等的四边形是平行四边形
(4)定理3:对角线互相平分的四边形是平行四边形
(5)定理4:一组对边平行且相等的四边形是平行四边形
4、两条平行线的距离
两条平行线中,一条直线上的任意一点到另一条直线的距离,叫做这两条平行线的距离。
平行线间的距离处处相等。
5、平行四边形的面积:S平行四边形=底边长×高=ah
典型例题1:
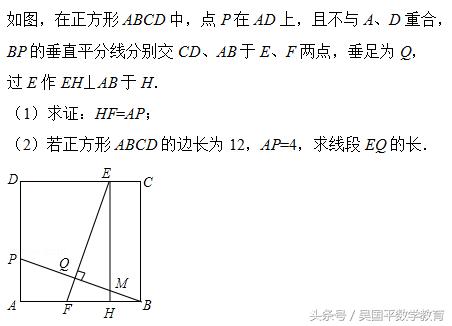

考点分析:
正方形的性质;全等三角形的判定与性质;勾股定理.所有
题干分析:
(1)先根据EQ⊥BO,EH⊥AB得出∠EQN=∠BHM=90°.根据∠EMQ=∠BMH得出△EMQ∽△BMH,故∠QEM=∠HBM.由ASA定理得出△APB≌△HFE,故可得出结论;
(2)由勾股定理求出BP的长,根据EF是BP的垂直平分线可知BQ=1/2BP,再根据锐角三角函数的定义得出QF=BQ的长,由(1)知,△APB≌△HFE,故求出EF=BP的值,再根据EQ=EF﹣QF即可得出结论.
解题反思:
本题考查的是正方形的性质,熟知正方形的性质及全等三角形的判定与性质是解答此题的关键.
四边形知识内容(一般包括平行四边形、矩形、正方形、菱形)是初中数学几何主要考查部分,也是每年中考必考的几何考点。
同时,跟四边形相关的还常常以数与形、代数计算与几何证明、相似三角形的判定与性质、画图分析与列方程求解、勾股定理与函数、圆和三角相结合的综合性试题出现。
在一些综合问题中还会考查到一些数学思想:如数形结合思想、分类讨论思想、几何运动变化等数学思想。

三、矩形相关知识概念
1、矩形的概念
有一个角是直角的平行四边形叫做矩形。
2、矩形的性质
(1)具有平行四边形的一切性质
(2)矩形的四个角都是直角
(3)矩形的对角线相等
(4)矩形是轴对称图形
3、矩形的判定
(1)定义:有一个角是直角的平行四边形是矩形
(2)定理1:有三个角是直角的四边形是矩形
(3)定理2:对角线相等的平行四边形是矩形
4、矩形的面积
S矩形=长×宽=ab

四、菱形相关知识概念
1、菱形的概念
有一组邻边相等的平行四边形叫做菱形
2、菱形的性质
(1)具有平行四边形的一切性质
(2)菱形的四条边相等
(3)菱形的对角线互相垂直,并且每一条对角线平分一组对角
(4)菱形是轴对称图形
3、菱形的判定
(1)定义:有一组邻边相等的平行四边形是菱形
(2)定理1:四边都相等的四边形是菱形
(3)定理2:对角线互相垂直的平行四边形是菱形
4、菱形的面积
S菱形=底边长×高=两条对角线乘积的一半
典型例题2:



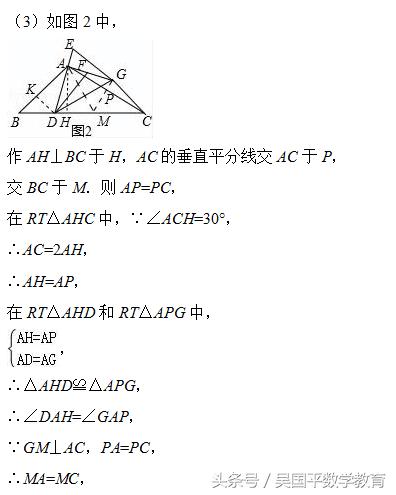

题干分析:
(1)如图1中,过点A作AH⊥BC于H,分别在RT△ABH,RT△AHC中求出BH、HC即可.
(2)如图1中,过点A作AP⊥AB交BC于P,连接PG,由△ABD≌△APG推出BD=PG,再利用30度角性质即可解决问题.
(3)如图2中,作AH⊥BC于H,AC的垂直平分线交AC于P,交BC于M.则AP=PC,作DK⊥AB于K,设BK=DK=a,则AK,AD=2a,只要证明∠BAD=30°即可解决问题.
解题反思:
本题考查相似三角形综合题、全等三角形的判定和性质、直角三角形30度角性质、线段垂直平分线性质等知识,解题的关键是添加辅助线构造全等三角形,学会设参数解决问题,属于中考压轴题.
五、正方形相关知识概念
1、正方形的概念
有一组邻边相等并且有一个角是直角的平行四边形叫做正方形。
2、正方形的性质
(1)具有平行四边形、矩形、菱形的一切性质
(2)正方形的四个角都是直角,四条边都相等
(3)正方形的两条对角线相等,并且互相垂直平分,每一条对角线平分一组对角
(4)正方形是轴对称图形,有4条对称轴
(5)正方形的一条对角线把正方形分成两个全等的等腰直角三角形,两条对角线把正方形分成四个全等的小等腰直角三角形
(6)正方形的一条对角线上的一点到另一条对角线的两端点的距离相等。
3、正方形的判定
(1)判定一个四边形是正方形的主要依据是定义,途径有两种:
先证它是矩形,再证有一组邻边相等。
先证它是菱形,再证有一个角是直角。
(2)判定一个四边形为正方形的一般顺序如下:
先证明它是平行四边形;
再证明它是菱形(或矩形);
最后证明它是矩形(或菱形).

六、梯形相关知识概念
1、梯形的相关概念
一组对边平行而另一组对边不平行的四边形叫做梯形。
梯形中平行的两边叫做梯形的底,通常把较短的底叫做上底,较长的底叫做下底。
梯形中不平行的两边叫做梯形的腰。
梯形的两底的距离叫做梯形的高。
两腰相等的梯形叫做等腰梯形。
一腰垂直于底的梯形叫做直角梯形。
2、梯形的判定
(1)定义:一组对边平行而另一组对边不平行的四边形是梯形。
(2)一组对边平行且不相等的四边形是梯形。
3、等腰梯形的性质
(1)等腰梯形的两腰相等,两底平行。
(3)等腰梯形的对角线相等。
(4)等腰梯形是轴对称图形,它只有一条对称轴,即两底的垂直平分线。
4、等腰梯形的判定
(1)定义:两腰相等的梯形是等腰梯形
(2)定理:在同一底上的两个角相等的梯形是等腰梯形
(3)对角线相等的梯形是等腰梯形。
几何综合问题一直是很多考生的“恶梦”,此类题型不仅要求考生具有一定层次、深度的推理过程,更考查考生的逻辑思维能力、基本图形分析能力和数学语言的表达能力等等,自然这类题型受到命题老师的青睐。同时几何论证题也是中考压轴题的背景和铺垫,函数型综合题和几何型综合题都是以几何图形为背景的。
,




