大多数朋友对于相对论的认知都起源于中学时期,物理课本上会有几个小节为大家介绍相对论的基本思想和结论,因为不是考试重点,这部分内容也就草草了之了,但“爱因斯坦 相对论”这俩如此有名的招牌,肯定会吸引不少学生自己去琢磨一些问题,正是因为如此,一些似是而非的判断出现了。

小明问道:“假设有一艘宇宙飞船从地球发射,做匀加速直线运动,飞往遥远的宇宙深处,试问宇宙飞船上的时间流速与地球有差异吗?”
小刚回答:“老师和课本上都说了,狭义相对论只适用于惯性参考系,你说的宇宙飞船一直处于加速状态,不符合狭义相对论的要求,因此这道问题没法用狭义相对论求得。”
“不过我看课本上有介绍过广义相对论,其中的等效原理似乎可以简单的回答这个问题”小刚略有迟疑的继续说着。
“等效原理告诉我们加速度和引力等效,那么这个匀加速飞船,其内部不就相当于产生了一个引力场吗?这样一来,宇宙飞船内部的时间流速应该可以用广义相对论求出来!可惜这么高深的问题,我们现在还不会计算”
上面我们通过模拟两位同学的对话,介绍了这个例子,对于小刚的思路,我猜测不少朋友也都这么想过(没错,说的就是我自己,当初我就是这么想的),甚至于还因为得出这样的结论而感到“震惊和高兴”。

按照大多数文章的讲述顺序,这里应该到了反驳环节,本篇文章自然也不例外。
例子当中小刚的思路虽然乍一看合情合理,但实际上这里的问题完全与广义相对论无关。虽然课本上说明了狭义相对论适用于惯性参考系,但谁说它不能用于惯性系中的非惯性运动了吗?否则我们凭什么可以在建立于伽利略变换之上的牛顿力学中毫无顾忌的思考加速运动?(我们要知道,牛顿力学的适用范围也是惯性系,这一点想必所有人都知道)

考虑到这点之后,是否有些小惊?现在我们就说清楚一点,所谓的狭义相对论只适用于惯性参考系,那是指使用者必须从惯性观察者的角度考虑问题,也就是若如果你的运动状态一直处于静止或者匀速,那么你所看到的一切物理现象都可以应用狭义相对论(如果这些物理现象处于狭义相对论范围内的话)。
补充一点刚才的说法按照现代相对论观点来看,实际上是错的或者说不严谨。因为在很多非专业教材里对狭义相对论和广义相对论的区分,仍旧停留在惯性系与非惯性系之间,这是相对论早期看法,而经过这么多年的发展,这个看法早已被淘汰(毕竟当时要对惯性系下个严格定义都很难,循环论证)
至于现代看法,很简单,也很本质,那就是看背景时空是否弯曲,平直的属于狭义相对论,弯曲的属于广义相对论(当然了,这里的狭义相对论所包含的内容将比我们习惯中的那个以洛伦兹变换为核心的狭义相对论多的多,甚至于你还可以从更高的角度去看,狭义相对论只是广义相对论在平直时空下的形式,可以说相对论只有一个,那就是广义相对论)。

如果按照时空是否弯曲的角度考虑,狭义相对论实际上是可以适用于所有参考系的,不管它是惯性的还是非惯性的,比如例子中作匀加速运动的飞船这一非惯性系,就可以从被称为Rindler的坐标系中进行讨论。
不过对于这个话题,本篇文章就不做更多的讨论了,我们就还按照此前的说法,看看到底如何用狭义相对论解决小明的问题。
既然狭义相对论可以处理非惯性运动,那么例子中作匀加速直线运动的宇宙飞船的时间流速又该如何计算呢?
以洛伦兹变换为基础(虽然洛伦兹变换是建立在两个惯性系之上,但我们对于作加速运动物体的移动轨迹上可以设置无穷个瞬时惯性系,物体在每个瞬时惯性系中速度为零),我们最终可推出如下公式:

这是地球时间和飞船时间之间的关系,其中T代表地球时间,t代表飞船时间,c代表光速,a代表飞船加速度。
这里需要说明一下的是,这个a代表飞船加速度,数据是由飞船内部人员给出的(大家可以想想这个加速度有什么办法可以测得),因此这个加速度可以被称为固有加速度,由于问题的前提条件是匀加速,所以这个固有加速度数值从始至终都没有变化过。
提到固有加速度,那是不是还有其它加速度呀?没错,上段特地强调了固有加速度是飞船内部人员测出来,是个常数,但这个加速度对外可就不是常数了,比如说地球人测得的飞船加速度,如下公式:
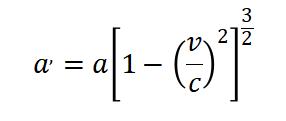
这个公式实际上是上边公式推导过程的中间产物,公式左侧a'代表地球人测得的飞船加速度,我们可以清楚的看到,随着飞船速度的上升,地球测到的飞船加速度正在不断减小(但飞船自身的固有加速度始终没变),这也说明了,在地球人眼中,飞船的速度永远到达不了光速。
至此,小明的问题也有了解答,那就是作匀加速运动的宇宙飞船,其内部时间流逝的速度是要慢于地球的,如果这个飞船日后还要返回的地球的话,那么会发现飞船里的宇宙员相比于地球上的朋友,都显的还很年轻。

似乎还缺少点什么,我们上述内容只是介绍了狭义相对论如何处理加速运动,但记得例子中小刚还给出为什么加速运动要用广义相对论解决的理由,虽然这个理由是错的,但我们最后还是简单的解释下原因吧。
虽然飞船作的是加速运动,并且飞船内部人员实实在在的感受到了加速,但这不是应用等效原理的理由(或者说等效原理被曲解用歪了),因为等效原理说的是均加速场等效于均引力场,而这个均引力场是不存在的,因为在广义相对论中,引力场可以用潮汐效应是否存在而进行判断,但所谓的均引力场中是没有潮汐效应的,所以加速度和真正的引力并没有什么关系。

综上所述,对于引力场可忽视的情况下,加速直线运动(非惯性运动),狭义相对论可以很好的解决,用不着广义相对论出手,即便出手的话,也还是要回到狭义相对论,毕竟狭义相对论是广义相对论在平直时空下的形式。

题目中说到匀速直线运动,而上文只介绍了加速直线运动,那么对于非直线运动又是如何呢?我们将于下篇文章介绍“爱因斯坦转盘”相关内容。
本篇文章的内容到此结束。
谢谢各位阅读!
以后还会不断更新精心准备的通俗科普长文!
期待您的点评和关注哦!,




