今天我想分享给大家汉诺塔问题的一个巧妙的解法,它只用到了另一个计数系统中的数数过程,而且它竟还能帮你找到填充谢尔宾斯基三角形的一条曲线。本来我不是喜欢小谜题和小游戏的那类人,不过我就是爱看这些谜题的解析,也爱看其中的数学规律,并且思考这究竟是怎么来的。要是你不熟悉这个的话,我们首先解释一下什么是汉诺塔问题。

我们有三根柱子,还有从大到小的几个圆盘,这些圆盘都被穿了孔,这样就可以被串到柱子上。这里我画了5个圆盘,依次标记为0 1 2 3 4。不过理论上你想放多少个圆盘都行。一开始圆盘从大到小依次叠放在一根杆上,你的目标是把整个塔从一根杆子移动到另一根杆子上。它的规则是,一次只能移动一个圆盘,而且大圆盘不能叠在小圆盘上面。例如,第一步你只能移动0号圆盘,因为其他盘上面都有东西,不先移开的话它们是动不了的。接下来,你可以移动1号盘,但它只能移动到没有0号盘的柱子上,不然大圆盘会被放到小圆盘的上面,这就犯规了。

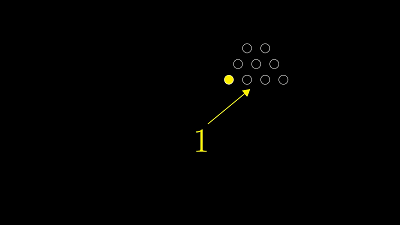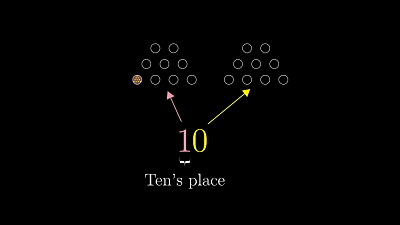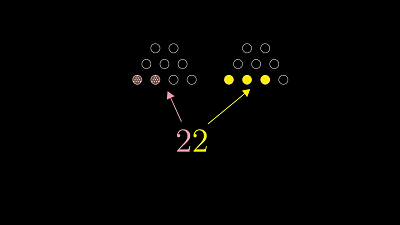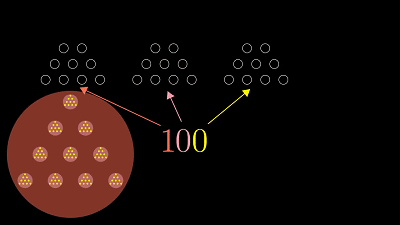
第一次听说这游戏的同学们,我强烈建议你们暂停视频,拿出不同大小的书本,自己试试看,感受感受这个问题。假如你认为它难的话,难在哪里?简单的话,简单在哪里?想想这样的问题。令人惊讶的是想解开汉诺塔问题,你只需要用二进制来数数,然后用计数的节奏来对应出移动圆盘的节奏。要是你不熟悉二进制的话,我首先会简短地概括一遍。其实,就算你已经很懂二进制,我还是想着重解释一下用它计数时的节奏,因为你以前说不定没这样想过。一般我们解释二进制时,首先会重新审视我们平常表示数字的方法,也就是十进制。因为我们会用到十个不同的数字,从0到9。这样数数的节奏是,首先把十个数字都数一遍,当每个数字都用完之后,你需要数"十",于是用2位数来表示:一零,这个"1"位于十位,因为它代表了你之前数过的那十个数。然后把个位数清零,变成0。数数的节奏是这样重复的:数到9 然后十位进1,再数9个数然后十位再进1,如此类推。直到重复9遍之后,你就会向百位进1,百位记录的是你数过了多少个一百,这时后两位数就被清零了。
从这个角度看,计数的节奏有点自相似性:即使在更大的尺度上,整个过程也还是这样的,做一个动作进一位,做同样的动作再进一位,重复9次之后再进更大的一位。在二进制中你只能用两个数字 0和1,它们叫比特,这其实是"二进制数位"的简称。这样一来,计数时你就得经常进位了。当你数完0和1后,比特就全用完了,于是你就要进到二位写作"10"。习惯了十进制的你千万要忍住别把它读作"十",而是要把它想成是1个二加上0,下一个数是11,表示数字三。接着你就又要进位了,但二位上已经是1了,所以你得再进一位。结果就是100,表示1个四,加0个二,加0。十进制里的数位表示10的幂,同理二进制中的数位表示不同的2的幂。因此,十进制中有十位、百位、千位等等的概念。在二进制中有二位、四位、八位等等的概念。

于是数数的节奏就快了很多,不过同时也变得更加明显了,末位加一,进一位;末位再加一,进两位;末位又加一,进一位;末位再加一,进三位。这个规律再次展现了自相似性,在不同的尺度上,这个过程都是做一个动作,进位再重复动作。在小尺度下,例如数到三,也就是二进制中的11,我们先让个位数加一,然后进到二位,再让个位数加一。在大尺度上,例如数到十五,也就是二进制的1111,则先让后三位数数到七,进到八位,然后再让后三位数到七,数到255也就是二进制里的8个1的话,你需要先数完最后7个比特,进到128位,然后再数完最后7个比特。

好了,说完了二进制简介,我们可以给出惊人的事实是,能用这个节奏解开汉诺塔问题。你从零开始数起,每当你只是把末位数从0变成1的时候,就把0号盘移到它右边的柱子上,如果0已经在最右的柱子上了 就把它移回第一根柱子,要是在二进制计数中,你进到了二位,也就是把末两位数从01变成10的话,你就移动1号盘,也许你会问移到哪里呢?其实,你并没有什么选择,你不能把它放到0号上,而剩下的只有另一根柱了。所以你该往哪里移就往哪里移,接下来数到11,只需要个位加一,于是你再次移动0号盘,然后二进制中进到四位,所以你移动2号圆盘,接下来的规律是类似的。个位加一,移动0号盘,二位进一,移动1号盘,末位加一,移动0号盘,接着我们要进位三次,到八位,相应地我们移动3号圆盘。这个解法相当奇妙,我第一次看到的时候在想,这不可能。我不懂这个原理,不懂为什么能行,现在我懂了,不过看一遍还是觉得奇妙。我记得曾经制作了一个动画演示,怎么说呢,我懂得原理,知道发生了什么。但坐下来完整地看一遍,还是觉得很有意思?

你想想,一开始你都说不准为什么每一步都不会犯规,例如怎么保证每次进到八位时3号盘都一定能够移动呢?同时,这个解法马上引出了其他的问题。例如这是怎么来的,为什么能行?有没有比2的(n-1)次方步更快的解法呢?其实这个解法不仅能解汉诺塔问题,而且还是个最优解。想要理解这为什么,怎么能行,究竟是什么道理,你得用某一个思想来看这个谜题,这个思想在计算机科学里叫做递归。3号盘心想,210你们好,你们挪个地儿呗。这么大堆玩意儿搁我身上叫我可咋整,于是从3号盘的角度想,你要是想要移动3号的话,不管你怎么做 2 1 0号盘必须得移动到B柱,它们必须得这么挪,任何一个盘在3号上面的话,3号都动不了。任何盘在C柱上的话 3号就不能移过去了,所以我们得移开2 1 0号,这样以后,我们就可以把3号移到C柱。然后3号说,我完事儿了,干啥都别捣鼓我了,你们能耐就都往我身上堆。于是,你就会得到同一个更小的问题。现在0 1 2号盘在B柱上,要把它们移动到C柱上,所以思路是,每次只看一个圆盘,然后想,要移动这个盘必须做什么。这样我就把大问题变成小一点的问题了,那小问题怎么解呢?一模一样的道理,2号盘说,1号0号,你们那个我不是说谁,就是我想要一点空间,请下去吧。1号0号得移走,2号就能到想去的地方了,然后1号0号再移回来。重点是每个圆盘的策略都是一样的,它们都说。楼上的下来。然后我就要动了。好之后大家就可以回来了,想到这个要点之后,你就能写出解汉诺塔的代码了,也就是五六行的事。估计这是史上每一行动脑量最大的代码,多想一想的话,你会发现这明显是最高效的解法。

在每一步上,你做的不过是你必须要做的事,在移动3号之前,必须移开0到2号,然后你必须移动3号,然后你必须把0到2号移回来。这样看,根本没有浪费步数的余地。那为什么二进制计数可以表示这个算法呢?是这样的,解决小问题,移动大圆盘,再解决小问题的这个规律,跟二进制计数是完全一致的。即数到一个数,进位,再数到同一个数。而且汉诺塔的算法和二进制计数都是自相似的过程,我的意思是,要是你多数一些,数到2的更高次幂,或者解圆盘数更多的汉诺塔,两者的结构都是一样的:子问题,动一步什么,同样的子问题。举个例子,解两个圆盘的汉诺塔时,移动0号,移动1号,移动0号,对应着用二进制来数到三。末位加一,进一位,末位加一。大一点的例子,3个圆盘的汉诺塔是这样解的,想办法解决2个盘的问题:移动2号盘,再想办法解决2个盘的问题。同样地,二进制中数到111,要先数三个数到11,最高位进一,再数三个数,在任何尺度下,两个过程的结构是一样的。

所以可以说,二进制解法可行的原因,至少是原因之一吧,并没有唯一的正确解释。但我觉得最自然的解释是,写出这些二进制数所用到的规律和解决汉诺塔问题所用到的规律,结构是一模一样的。因此如果你去看比特的跳动方式,你实际上是在反过来思考,也就是在问,二进制数是怎么写出来的。就像当我想要理解比特是如何通过跳动来解答的时候,实际上你就是在逆向地找出汉诺塔的递归算法,这就是解法成功的原因。很酷对吧,不过其实还有更酷的,以后有机会的话我们再讲这和谢尔宾斯基三角形之间的关系。
,