有关√2,,√3,√5 ,圆周率π的连分式你已经很熟悉了,它们都比较简单,但你见过三角函数的连分式吗,本篇我们就来探讨三角函数tanx的连分式
首先回忆下√2的连分式,如下图

超越数e的连分式,
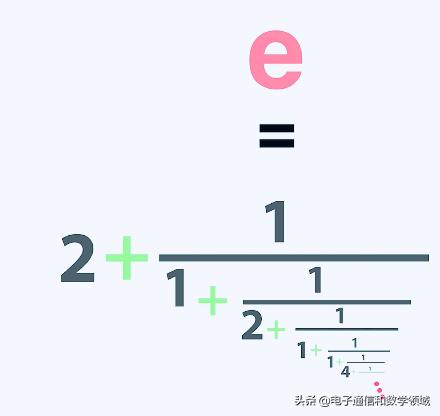
有理数的连分式,注意:有理数的连分式是有限的,不会像无理数或超越数那样无限延伸下去

如下是tanX的三角函数,它可以写成

接着,我们引入正弦和余弦函数的级数形式

所以tanX可写成sinX/cosX的级数之比,

我们可以提取一个X项

像求无理数连分式一样,将分子分母写成倒数的形式,如下图:这是常用的一种方法


接着进入关键的一步:如下在分子上同时加上或减去一个级数,如下蓝色部分所示

我们交换顺序,如下紫色部分所示,

然后对其进行运算,如下首项合并后为0

第二项合并等于(2X^2)/(1*2*3),如下图


接着同理我们合并第三项,第四项得到

最终就等于紫色区域所示的结果

我们继续化简,分子/分母化简得到,这时整数项就有一个1

我们还可以提取一个X^2,并消去多余的公共项,如下图所示,

所以就得到了如下最终的结果

我们继续运用前面所述的原理,分子分母写成倒数的形式,如下图

我们继续循环下去,因篇幅较长,下一篇我们继续讨论。
,




