



































第一单元:小数乘法
1、小数乘整数:意义——求几个相同加数的和的简便运算。
如:1.5×3表示1.5的3倍是多少或3个1.5是多少。
计算方法:先把小数扩大成整数;按整数乘法的法则算出积;再看因数中一共有几位小数,就从积的右边起数出几位点上小数点。
2、小数乘小数:意义——就是求这个数的几分之几是多少。
如:1.5×0.8(整数部分是0)就是求1.5的十分之八是多少。
1.5×1.8(整数部分不是0)就是求1.5的1.8倍是多少。
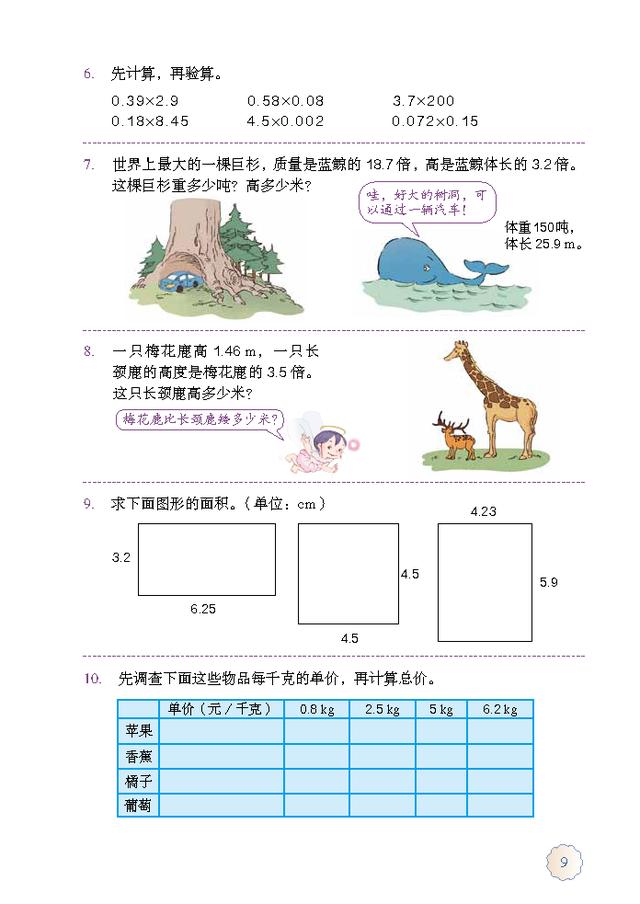
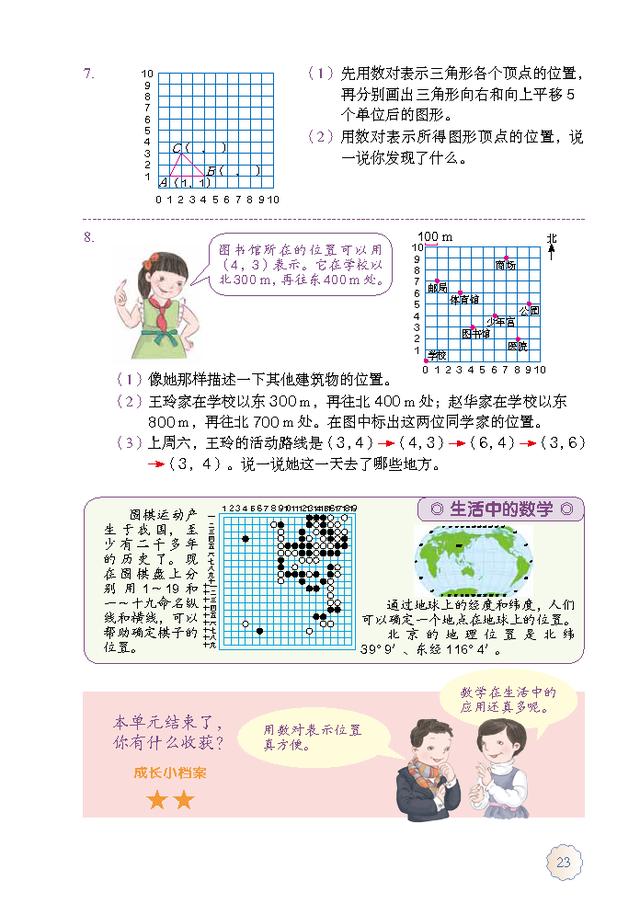
计算方法:先把小数扩大成整数;按整数乘法的法则算出积;再看因数中一共有几位小数,就从积的右边起数出几位点上小数点。
注意:计算结果中,小数部分末尾的0要去掉,把小数化简;小数部分位数不够时,要用0占位。
3、规律:一个数(0除外)乘大于1的数,积比原来的数大; 一个数(0除外)乘小于1的数,积比原来的数小。
4、求近似数的方法一般有三种:
⑴四舍五入法;⑵进一法;⑶去尾法
5、计算钱数,保留两位小数,表示计算到分。保留一位小数,表示计算到角。
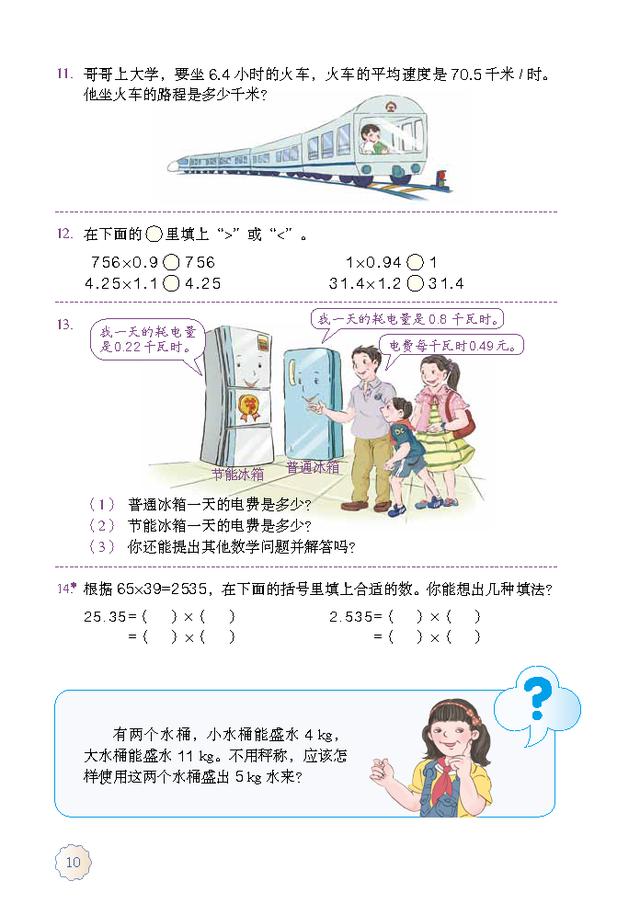
6、小数四则运算顺序跟整数是一样的。
7、运算定律和性质:
加法:加法交换律:a b=b a
加法结合律:(a b) c=a (b c)
乘法:乘法交换律:a×b=b×a
乘法结合律:(a×b)×c=a×(b×c)见2.5找4或0.4,见1.25找8或0.8
乘法分配律:(a b)×c=a×c b×c或a×c b×c=(a b)×c(b=1时,省略b)
变式: (a-b)×c=a×c-b×c或a×c-b×c=(a-b)×c
减法:减法性质:a-b-c=a-(b c)
除法:除法性质:a÷b÷c=a÷(b×c)
第二单元:位置
8、确定物体的位置,要用到数对(先列:即竖,后行即横排)。用数对要能解决两个问题:一是给出一对数对,要能在坐标途中标出物体所在位置的点。二是给出坐标中的一个点,要能用数对表示。
第三单元:小数除法
10、小数除法的意义:已知两个因数的积与其中的一个因数,求另一个因数的运算。如:0.6÷0.3表示已知两个因数的积0.6,一个因数是0.3,求另一个因数是多少。
11、小数除以整数的计算方法:小数除以整数,按整数除法的方法去除,商的小数点要和被除数的小数点对齐。整数部分不够除,商0,点上小数点。如果有余数,要添0再除。
11、除数是小数的除法的计算方法:先将除数和被除数扩大相同的倍数,使除数变成整数,再按“除数是整数的小数除法”的法则进行计算。
注意:如果被除数的位数不够,在被除数的末尾用0补足。
12、在实际应用中,小数除法所得的商也可以根据需要用“四舍五入”法保留一定的小数位数,求出商的近似数。
13、除法中的变化规律:①商不变性质:被除数和除数同时扩大或缩小相同的倍数(0除外),商不变。②除数不变,被除数扩大(缩小),商随着扩大(缩小)。③被除数不变,除数缩小,商反而扩大;被除数不变,除数扩大,商反而缩小。
14、(P28)循环小数:一个数的小数部分,从某一位起,一个数字或者几个数字依次不断重复出现,这样的小数叫做循环小数。 循环节:一个循环小数的小数部分,依次不断重复出现的数字。如6.3232……的循环节是32.简写作6.32
15、小数部分的位数是有限的小数,叫做有限小数。小数部分的位数是无限的小数,叫做无限小数。小数分为有限小数和无限小数。
第四单元:可能性
16、事件发生有三种情况:可能发生、不可能发生、一定发生。
17、可能发生的事件,可能性大小。把几种可能的情况的份数相加做分母,单一的这种可能性做分子,就可求出相应事件发生可能性大小。
第五单元:简易方程
18、在含有字母的式子里,字母中间的乘号可以记作“·”,也可以省略不写。加号、减号除号以及数与数之间的乘号不能省略。
19、a×a可以写作a·a或a ,a 读作a的平方 2a表示a a
特别地1a=a这里的:“1“我们不写
20、方程:含有未知数的等式称为方程(★方程必须满足的条件:必须是等式 必须有未知数两者缺一不可)。使方程左右两边相等的未知数的值,叫做方程的解。求方程的解的过程叫做解方程。
21、解方程原理:天平平衡。 等式左右两边同时加、减、乘、除相同的数(0除外),等式依然成立。
22、10个数量关系式:加法 和=加数 加数 一个加数=和-另一个加数
减法:差=被减数-减数 被减数=差 减数 减数=被减数-差
乘法:积=因数×因数 一个因数=积÷另一个因数
除法:商=被除数÷除数 被除数=商×除数 除数=被除数÷商
23、所有的方程都是等式,但等式不一定都是等式。
24、方程的检验过程:方程左边=……
25、方程的解是一个数; 解方程式一个计算过程。=方程右边 所以,X=…是方程的解。
第六单元:多边形的面积
26、公式:
多边形
面积公式
面积公式的变式
说明
正方形
正方形的面积=边长X边长 S正=aXa=a2
已知:正方形的面积,求边长
长方形
长方形的面积=长X宽
S长=aXb
已知:长方形的面积和长,求宽
平行四边形
平行四边形的面积=底X高
S平=aXh
已知:平行四边形的面积和底,求高 h=S平÷a
三角形
三角形的面积=底X宽高÷2
S三=aXh÷2
已知:三角形的面积和底,求高
H=S三X2÷a
梯形
梯形形的面积=(上底 下底)X高÷2
S梯=(a b)X2
已知:梯形的面积与上下底之和,求高
高=面积×2÷(上底 下底)
上底=面积×2÷高-下底
组合图形
当组合图形是凸出的,用两种或三种简单图形面积相加进行计算。
当组合图形是凹陷的,用一种最大的简单图形面积减较小的简单图形面积进行计算。
27、平行四边形面积公式推导:剪拼、平移
平行四边形可以转化成一个长方形;长方形的长相当于平行四边形的底; 长方形的宽相当于平行四边形的高;
长方形的面积等于平行四边形的面积,因为长方形面积=长×宽,所以平行四边形面积=底×高。
28、三角形面积公式推导:旋转
两个完全一样的三角形可以拼成一个平行四边形,平行四边形的底相当于三角形的底;平行四边形的高相当于三角形的高;
平行四边形的面积等于三角形面积的2倍,因为平行四边形面积=底×高,所以三角形面积=底×高÷2
29、梯形面积公式推导:旋转
30、两个完全一样的梯形可以拼成一个平行四边形。平行四边形的底相当于梯形的上下底之和;平行四边形的高相当于梯形的高;平行四边形面积等于梯形面积的2倍,因为平行四边形面积=底×高,所以梯形面积=(上底 下底)×高÷2
31、等底等高的平行四边形面积相等;等底等高的三角形面积相等;
等底等高的平行四边形面积是三角形面积的2倍。
32、长方形框架拉成平行四边形,周长不变,面积变小。
33、组合图形面积计算:必须转化成已学的简单图形。
当组合图形是凸出的,用虚线分割成几种简单图形,把简单图形面积相加计算。
当组合图形是凹陷的,用虚线补齐成一种最大的简单图形,用最大简单图形面积减几个较小的简单图形面积进行计算。
第七单元:数学广角——植树问题
34、不封闭栽树问题:
(1)一条路的一边两端都栽树=路长÷间隔 1;
已知间隔数,树的棵树,求路长。路长=间隔数×(树的棵树-1)
(2)一条路的两边两端都栽树=(路长÷间隔 1)×2
(3)一条路的一边两端不栽树=路长÷间隔-1
(4)一条路的两边两端不栽树=(路长÷间隔-1)×2
(5)锯木头时间问题:锯一段木头时间=总时间÷(段数-1)
35、封闭图形四周栽树问题:栽树棵树=周长÷间隔
36、鸡兔同笼问题:(龟鹤问题、大船小船问题)
(1)算术假设法1:假设几只都是兔子,(都是脚多的兔子),先求鸡的只数
鸡的只数:(总头数×4-总脚数)÷(4-2即一只兔的脚数减去一只鸡的脚数)
兔的只数:总头数-鸡的只数
算术假设法2:假设几只都是鸡,(都是脚少的鸡),先求兔子的只数
兔子的只数:(总脚数-总头数×2)÷(4-2即一只兔的脚数减去一只鸡的脚数)
鸡的只数:总头数-兔子的只数
(2)方程法:设兔子有x只,则兔子脚有2x只。那么鸡有(总头数-x)只
根据“兔子脚 鸡脚=总脚数”列方程解答先求兔子只数,再算出鸡的只数。
即:4x 2×(总头数-x)=总脚数
补充内容:观察物体
36、从不同的角度观察物体,看到的形状可能是不同的;观察长方体或正方体时,从固定位置最多能看到三个面。(习惯上我们从左面、正面、上面看 ,把这三种视图统称三视图)
37、图形的运动:轴对称图形。
(1)沿一条直线对折后,两边完全重合的图形叫做轴对称图形,这条直线叫做对称轴。圆有无数条对称轴。正方形有4条对称轴。等边三角形有3条对称轴。长方形有2条对称轴。等腰三角形和等腰梯形有1条对称轴。
(2)轴对称图形的特点:沿对称轴对折,两边完全重合。每一组对应点到对称轴距离度相等。对应点之间的连线与对称轴互相垂直。
(3)要能根据对称轴画出对称图形的另一半。
38、数字编码:
(1)数不仅可以用来表示数量和顺序,还可以用来编码。
(2)邮政编码由6位数字组成,前2位表示省;前3位表示邮区,前4位表示县市,最后2位表示投递局(大地基乡投递局)
(3)身份证18位:第7至14位表示出生年月日 倒数第二位的数字表示性别,单数-男,双数-女
(4)根据卡号信息、运动员编号信息、门牌信息填写编码规律。
易错题练习01 填空题。
1、1.25×0.8表示( )。
2、去掉0.25的小数点,就是把这个数扩大( );把50.4的小数点向左移动两位,就是把它缩小到原来的( )。
3、两个因数相乘,一个因数扩大10倍,另一个因数扩大3倍,积会( )。
4.一个不为0的数乘以0.8,它的积比这个数( )。一个自然数乘以0.01,就是把这个自然数( )。
5、把“2.58×0.03”中的0.03扩大为3而使积不变,另一个因数2.58的小数点应( ),积保留两位小数是( )。
6、56÷11的商用循环小数表示是( )精确到百分位是( )。
7、3÷11的商用循环小数的简便写法记作( ),商保留一位小数是( )。
8、9.97÷4.21的商保留两位小数是( ),保留整数是( )。
9、在“80.904;80.409;80.049”中,最小的是( ),最大的是( )。
10、两个因数的积是3.4,如果把两个因数同时扩大10倍,积是( )。
11、三个2.5连乘得积是( )。
12、3x=6.9的解是( )。
13、水果店运来香蕉x千克,运来的桃子是香蕉的2.5倍,香蕉和桃子一共运来( )千克。如果x=5,桃子比香蕉多( )千克。
14、35dm2=( )cm2;7.4m2=( )dm2;7.5m2=( )cm;2350m2=( )公顷;500平方米=( )公顷;3平方米70平方分米=( )平方米;3小时15分=( )小时;1.8时=( )时( )分;2.15小时=( )分钟;7.6米=( )米( )厘米。
15、把一个平行四边形木框拉成一个长方形,周长( ),它的高和面积都会( )
16、把一个长方形木框拉成一个平行四边形,周长( ),它的高和面积都会( )。
17、把一个平行四边形沿高剪开,重新拼成一个长方形,它的高和面积( ),周长( )。
18、一张边长是20厘米的正方形纸,从相邻两边的中点连一条线段(如下图),沿这条线段剪去一个角,剩下的(阴影部分)面积是( )cm2。
19、一个三角形和一个平行四边形底相等面积也相等。平行四边形的高是10cm,三角形的高是( )。
20、一个梯形的上底增加3厘米后就变成一个边长6厘米的正方形(如下图),这个梯形的面积是( )平方厘米。
21、把一个小数的小数点向右移动两位,得到一个新数,与原数相差44.55,原数是( )。
22、一个直角三角形的三条边分别是3cm、4cm和5cm,这个三角形的面积是( ),斜边上的高是( )。
23、一个小数有两位小数,保留一位小数它的近似值是10.0,这个数最大是( )最小( )。
24、三个连续自然数,中间的数是n,另外的两个数分别是( )和( )。
25、125缩小到它的( )是0.125;( )扩大到它的100倍是0.3。
26、一个两位数,它的个位上的数字是b,十位上的数字是a,那么这个两位数可写成( )。
27、一个等腰三角形的底是16cm,腰是a cm,高是b cm。这个三角形的周长是( )cm,面积是( )cm2。
28、一个等腰三角形的周长是16厘米,腰长是5厘米,底边上的高是4厘米,它的面积是( )平方厘米。
29、把一个边长8厘米的正方形剪拼成一个平行四边形后面积是( )。
30、0.25除以0.15,当商是1.6时,余数是( );0.79÷0.04,商是19,余数是( )。
31、一个梯形的上底、下底、高分别是5cm、9cm、6cm,面积是( )平方分米。
32、小明看见一个上底是15cm、下底是10cm、高是6cm的梯形摆着家里。这个梯形的面积是( )cm2。
33、一堆圆木,最顶层有5根,最底层有14根。每相邻两层相差1根圆木,这堆圆木一共有( )根。
34、一个三角形和一个平行四边形的面积相等,高也相等。如果三角形的底是25cm,平行四边形的底是( )dm。
35、一个直角梯形,如果把下底减少3cm,这个梯形就变成一个边长7cm的正方形。这个梯形的面积是( )cm2。
36、张诚把一个梯形的上底缩小成一点后 这个梯形就变成一个( )形。
02判断题。
1、小数乘法的意义和整数乘法的意义完全相同。( )
2、一个数乘0.8,积比原来的数小。( )
3、近似数7.0和7的大小相等,但精确度不一样。( )
4、8.4×0.5就是求8.4的一半是多少。( )
5、一个数除以一个小数,商可能是小数。( )
6、小数除以小数,商一定是小数。( )
7、在除法里:商一定小于被除数。( )
8、一个非0的数除以一个比1小的小数,所得的商一定比被除数大。( )
9、如果除数小于1,那么商就比被除数(0除外)大。( )
10、(0.1-0.1×0.1)÷0.1=0.9。( )
11、x2不可能等于2x。( )
12、a2>2a。( )
13、未知数的值叫做方程的解。( )
14、小数分有限小数、无限小数和循环小数。( )
15、一组数据的中位数和平均数可能相等。( )
16、循环小数不一定是无限小数。( )
17、方程左右两边同时乘一个相同的数,左右两边仍然相等。( )
18、把平行四边形木框拉成长方形,周长和面积都变大了。( )
19、如果两个图形能拼成平行四边形,那么它们一定完全一样。( )
20、边长是4分米的正方形,它的周长和面积相等。( )
21、两个都比1小的数(0除外)相乘,积一定小于其中的每一个因数。( )
22、方程5+2x=16.2的解是5.6。( )
23、6x+6=6(x+1)。( )
24、把一个梯形的上底、下底和高都扩大2倍,它的面积就扩大2倍。( )
03选择题。
1、a与它的2.5倍相差( )。
A、a-2.5 B、2.5-a C、1.5a
2、下面两个式子相等的是( )。
A、a a和2a B、a×2和a2 C、a a和a2
3、与3.75÷12.5结果相同的算式是( )。
A、3750÷12.5 B、37.5÷125 C、3750÷125
4、可以运用( )对4.7×99+4.7进行简便运算。
A、乘法交换律 B、乘法结合律 C、乘法分配律
5、已知两个因数的积是其中一个因数的3.5倍,是另一个因数的4.2倍,这两个因数的积是( )。
A、8.7 B、14.7 C、1.2
6、下面算式中积最小的是( )。
A、320×0.24 B、2.4×0.32 C、24×0.32
04列方程或算式。
1、“3.2除x的商是0.8”的等量关系式是__________________
2、一个数的3倍加上这个数的一半等于80.5,求这个数。
(列方程)解:设这个数是x,则方程是:__________________
3、一个数的5倍与它的3.6倍相差5.6,求这个数。
(列方程)解:设这个数是x,则方程是:__________________
4、“7与0.38的和去除4.6,商是多少?”的算式是__________________
05应用题。
1、某小学五年级有学生55个人。男生人数是女生人数的1.2倍。男、女生各有多少人?
2、童装厂原来做一种儿童服装,每套用布2.2米。现在改进了裁剪方法,每套节省布0.2米。原来做1800套这样的服装所用的布,现在可以多做几套?
3、一个长方形的周长是45厘米,长是宽的2倍。这个长方形的面积是多少平方厘米?
4、甲乙两筐苹果,甲筐苹果的个数是乙筐的2.4倍,如果从甲筐取出35个苹果放入乙筐,这时两筐苹果个数相等,原来两筐苹果各有多少个?(列方程解答)
5、妈妈将一些奶糖和水果糖分装在小袋里,每袋装入0.25千克奶糖和0.15千克水果糖。当水果糖用去4.5千克时,用去奶糖多少千克?
6、姐姐骑电瓶车每小时行18千米,弟弟开小汽车每小时行54千米。他俩从相距247千米的两地同时相向而行,2.5小时后两人还相距多少千米?
参考答案
01填空题。
1、1.25×0.8表示(1.25与0.8的积是多少)。
2、去掉0.25的小数点,就是把这个数扩大(100倍);把50.4的小数点向左移动两位,就是把它缩小到原来的(百分之一)。
3、两个因数相乘,一个因数扩大10倍,另一个因数扩大3倍,积会(30倍)。
4.一个不为0的数乘以0.8,它的积比这个数(小)。一个自然数乘以0.01,就是把这个自然数(缩小到这个自然数的百分之一或缩小100倍)。
5、把“2.58×0.03”中的0.03扩大为3而使积不变,另一个因数2.58的小数点应(向左移动两位),积保留两位小数是(0.08)。
6、56÷11的商用循环小数表示是(5.090909……),精确到百分位是(5.09)。
7、3÷11的商用循环小数的简便写法记作(),商保留一位小数是(0.3)。
8、9.97÷4.21的商保留两位小数是(2.37)保留整数是(2)。
9、在“80.904;80.409;80.049”中,最小的是(80.049),最大的是(80.904)。
10、两个因数的积是3.4,如果把两个因数同时扩大10倍,积是(340)
11、三个2.5连乘得积是(15.625)。
12、3x=6.9的解是(2.3)。
13、水果店运来香蕉x千克,运来的桃子是香蕉的2.5倍,香蕉和桃子一共运来(3.5x)千克。如果x=5,桃子比香蕉多(7.5)千克。
14、35dm2=(3500)cm2;7.4m2=(740)dm2;7.5m2=(75000)cm2;2350m2=(0.235)公顷;500平方米=(0.05)公顷;3平方米70平方分米=(3.7)平方米;3小时15分=(3.25)小时;1.8时=(1)时(48)分;2.15小时=(145)分钟;7.6米=(7)米(60)厘米。
15、把一个平行四边形木框拉成一个长方形,周长(不变),它的高和面积都会(变大)
16、把一个长方形木框拉成一个平行四边形,周长(不变),它的高和面积都会(变小)。
17、把一个平行四边形沿高剪开,重新拼成一个长方形,它的高和面积(不变),周长(变小)。
18、一张边长是20厘米的正方形纸,从相邻两边的中点连一条线段(如下图),沿这条线段剪去一个角,剩下的(阴影部分)面积是(350)cm2。
19、一个三角形和一个平行四边形底相等、面积也相等。平行四边形的高是10cm,三角形的高是(20cm)。
【解析:一个三角形和一个平行四边形在底相等,面积也相等的情况下,三角形的高是平行四边形的两倍。】
20、一个梯形的上底增加3厘米后就变成一个边长6厘米的正方形(如下图),这个梯形的面积是(27)平方厘米。
21、把一个小数的小数点向右移动两位,得到一个新数,与原数相差44.55,原数是(0.45)。【解析:把一个小数的小数点向右移动两位,原来小数扩大100倍,也就是增加99倍,所以原数是:44.55÷99=0.45】
22、一个直角三角形的三条边分别是3cm、4cm和5cm,这个三角形的面积是(6cm2),斜边上的高是(2.4cm)。【解析:直角三角形的三条边中,斜边是最长的,所以两条直角边分别3cm、4cm。两条直角边相当于这个直角三角形的底和高所以,三角形的面积=3×4÷2=6cm2,则斜边上的高=6×2÷5=2.4cm】
23、一个小数有两位小数,保留一位小数它的近似值是10.0,这个数最大是(10.04)最小(9.95)。
24、三个连续自然数,中间的数是n,另外的两个数分别是(n-1)和(n 1)。
25、125缩小到它的(千分之一)是0.125;(0.003)扩大到它的100倍是0.3。
26、一个两位数,它的个位上的数字是b,十位上的数字是a,那么这个两位数可写成(ab)。
27、一个等腰三角形的底是16cm,腰是a cm,高是b cm。这个三角形的周长是(2a 16)cm,面积是(8b)cm2。
28、一个等腰三角形的周长是16厘米,腰长是5厘米,底边上的高是4厘米,它的面积是(12)平方厘米。【解析:首先要求出,底=16-5×2=6cm,然后计算,面积=6×4÷2=12cm2】
29、把一个边长8厘米的正方形剪拼成一个平行四边形后面积是(64平方厘米)。【解析:用剪拼的方法改变了形状,面积是不会变的。只有用拉抻的方法改变形状,面积才会变。】
30、0.25除以0.15,当商是1.6时,余数是(10);0.79÷0.04,商是19,余数是(3)。
31、一个梯形的上底、下底、高分别是5cm、9cm、6cm,面积是(0.42)平方分米。【解析:注意面积单位的转化。】
32、小明看见一个上底是15cm、下底是10cm、高是6cm的梯形摆着家里。这个梯形的面积是(75)cm2。
33、一堆圆木,最顶层有5根,最底层有14根。每相邻两层相差1根圆木,这堆圆木一共有(95)根。【解析:本题关键是要算出这堆圆木的层数:14-5 1=10层,就可以计算圆木的根数:(5 14)×10÷2=95根】
34、一个三角形和一个平行四边形的面积相等,高也相等。如果三角形的底是25cm,平行四边形的底是(1.25)dm。【解析:注意长度单位。一个三角形和一个平行四边形在面积相等,高也相等的情况下,平行四边形的底只是三角形的一半。】
35、一个直角梯形,如果把下底减少3cm,这个梯形就变成一个边长7cm的正方形。这个梯形的面积是(59.5)cm2。
36、张诚把一个梯形的上底缩小成一点后 这个梯形就变成一个(三角)形。
02判断题。
1、小数乘法的意义和整数乘法的意义完全相同。(×)
【解析:
小数乘整数的意义与整数乘法的意义相同;而小数乘小数的意义与整数乘法的意义就不相同了;
补充:
整数乘法的意义:求几个相同加数的和的简便运算;
现有教材的理解已较宽:如3×4既可以说:3个4是多少?也可以表述成:4个3是多少?
小数乘法的意义:(原有老教材是分开的,供参考)
(1)小数乘整数:与整数乘法的意义相同,就是求几个相同加数的和的简便运算.例如:2.5×6 表示6个2.5求和或2.5的6倍是多少.
(2)一个数乘小数的意义:与整数乘法的意义有所不同,它是整数乘法意义的进一步扩展.它可以理解为是求这个数的十分之几、百分几、千分之几……是多少.例如,2.5 × 0.6表示2.5的十分之六是多少,2.5 × 0.98表示2.5的百分之九十八是多少.
记得现行教材统一为:就是求一个数的几倍(几分之几)是多少?
分数乘法的意义理解与小数乘法相同。】
2、一个数乘0.8,积比原来的数小。(×)
【解析:这个数只有大于0的时候,乘0.8,积才比原来的数小。】
3、近似数7.0和7的大小相等,但精确度不一样。(√)
【解析:对。根据四舍五入的规则,7.0在数值上等于7,但是在精确位上7.0的精确位是在最后一位,在十分位,7的精确位在个位,所以他们的精确位并不一样,即原题是对的。】
4、8.4×0.5就是求8.4的一半是多少。(√)
5、一个数除以一个小数,商可能是小数。(√)
6、小数除以小数,商一定是小数。(×)
7、在除法里:商一定小于被除数。(×)
8、一个非0的数除以一个比1小的小数,所得的商一定比被除数大。(√)
【解析:这道题如果局限在本册知识内,它就是对的;如果这个比1小的小数是个负数,那么所得的商就会比被除数小,如:2÷(-0.5)=-4,这时候原题就是错的。这道题出在小学阶段里,本身就没有意义。】
9、如果除数小于1,那么商就比被除数(0除外)大。(√)【解析:与上题同解。】
10、(0.1-0.1×0.1)÷0.1=0.9。(×)
11、x2不可能等于2x。(×)
【解析:如果x=2,那么x2就会等于2x】
12、a2>2a。(×)
【解析:只有a大于2时才是对的。如果a≤2,那么a2≤2a】
13、未知数的值叫做方程的解。(×)
【解析:错。正确的说法是:使方程左右两边相等的未知数的值叫做方程的解】
14、小数分有限小数、无限小数和循环小数。(×)
【解析:错。循环小数已经包含在无限小数中。小数分有限小数和无限小数两大类,而无限小数再分为无限循环小数和无限不循环小数。】
15、一组数据的中位数和平均数可能相等。(√)
【解析:正确。如1,2,3这组数里,2是中位数,也是平均数,是相等的。】
16、循环小数不一定是无限小数。(×)
【解析:错。循环小数本身就是无限小数。】
17、方程左右两边同时乘一个相同的数,左右两边仍然相等。(×)
【解析:等式的性质是:方程两边同时乘或除以同一个数(0除外),等式依然成立,题干中没说0除外,所以原题说法错误。】
18、把平行四边形木框拉成长方形,周长和面积都变大了。(×)
【解析:错。把平行四边形木框拉成长方形,四条边的长度是不会变的,所以周长不会变,只有面积变大了。】
19、如果两个图形能拼成平行四边形,那么它们一定完全一样。(×)
【解析:错。把一个平行四边形剪成一大一小的两个平行四边形来理解就明白了。】
20、边长是4分米的正方形,它的周长和面积相等。(×)
【解析:错。它们的数值虽然相同,但单位意义不一样,所以是不可能说周长和面积相等。】
21、两个都比1小的数(0除外)相乘,积一定小于其中的每一个因数。(√)
22、方程5+2x=16.2的解是5.6。(√)
23、6x+6=6(x+1)。(√)
【解析:对。根据乘法分配律,这个等式是成立的。】
24、把一个梯形的上底、下底和高都扩大2倍,它的面积就扩大2倍。(×)
【解析:错。假设原来的上底、下底、高分别是2cm、3cm、4cm,则面积是10平方厘米;上底、下底、高都扩大2倍后,上底、下底、高分别是4cm、6cm、8cm,面积是40平方厘米,面积不止扩大2倍,而是4倍了。】
03选择题。
1、a与它的2.5倍相差(C)。
A、a-2.5 B、2.5-a C、1.5a
【解析:2.5a-a=1.5a】
2、下面两个式子相等的是(A)。
A、a a和2a B、a×2和a2 C、a a和a2
【解析:a a和2a都表示两个a的和,所以这两个式子相等。】
3、与3.75÷12.5结果相同的算式是(B)。
A、3750÷12.5 B、37.5÷125 C、3750÷125
【解析:被除数与除数同时扩大10倍,商的大小不变。】
4、可以运用(C)对4.7×99+4.7进行简便运算。
A、乘法交换律 B、乘法结合律 C、乘法分配律
5、已知两个因数的积是其中一个因数的3.5倍,是另一个因数的4.2倍,这两个因数的积是(B)。
A、8.7 B、14.7 C、1.2
【解析:两个因数的积是其中一个因数的3.5倍(即另一个因数为3.5),是另一个因数的4.2倍(即这一个因数为4.2)则这两个因数的积是:3.5×4.2=14.7】
6、下面算式中积最小的是(B)。
A、320×0.24 B、2.4×0.32 C、24×0.32
【解析:不用计算,就用判断积的小数位数的方法来选择。】
04列方程或算式。
1、“3.2除x的商是0.8”的等量关系式是 x÷3.2=0.8
【解析:注意“除”跟“除以”是不同的。“除”表示它前面的数是除数,“除以”表示它前面的数是被除数。】
2、一个数的3倍加上这个数的一半等于80.5,求这个数。
(列方程)解:设这个数是x,则方程是: 3x x÷2=80.5
3、一个数的5倍与它的3.6倍相差5.6,求这个数。
(列方程)解:设这个数是x,则方程是: 5x-3.6x=5.6
4、“7与0.38的和去除4.6。商是多少?”的算式是 4.6÷(7 0.38)
05应用题。
1、某小学五年级有学生55个人。男生人数是女生人数的1.2倍。男、女生各有多少人
【解析:根据等量关系式 男生人数 女生人数=全班人数 列方程。】
解:设女生有x人,则男生有1.2x人
1.2x x=55
2.2x=55
x=55÷2.2
x=25
男生人数=1.2x=1.2×2.5=30(人)
答:(略)
2、童装厂原来做一种儿童服装,每套用布2.2米。现在改进了裁剪方法,每套节省布0.2米。原来做1800套这样的服装所用的布,现在可以多做几套?
【解析:要求现在可以多做几套,需知道原来做的套数(已知)与现在做的套数,要求现在做的套数,还需先求出布的总米数(1800×2.2)和现在每套用布的米数(2.2-0.2),然后算出现在可以做的套数1800×2.2÷(2.2-0.2)。由此找出条件列出算式解决问题】
1800×2.2÷(2.2-0.2)-1800=180(套)
答:(略)
3、一个长方形的周长是45厘米,长是宽的2倍。这个长方形的面积是多少平方厘米?
【解析:根据周长和已知长是宽的2倍这两个信息可以利用方程算出长和宽各是多少(根据“(长 宽)×2=长方形周长”这个长方形周长公式列出方程),然后就可以计算长方形的面积 。】
解:设宽是x厘米,则长是2x厘米。
(2x x)×2=45
3x=45÷2
3x=22.5
x=22.5÷3
x=7.5
则长=2x=2×7.5=15厘米
长方形的面积:15×7.5=112.5(平方厘米)
答:(略)
4、甲乙两筐苹果,甲筐苹果的个数是乙筐的2.4倍,如果从甲筐取出35个苹果放入乙筐,这时两筐苹果个数相等,原来两筐苹果各有多少个?(列方程解答)
解:设乙筐的苹果有x个,则甲筐的苹果有2.4x个。
2.4x-35=x 35
2.4x-x=35 35
1.4x=70
x=70÷1.4
x=50
则甲筐的苹果有:2.4x=2.4×50=120(个)
答:甲筐苹果有120个,乙筐苹果有50个。
5、妈妈将一些奶糖和水果糖分装在小袋里,每袋装入0.25千克奶糖和0.15千克水果糖。当水果糖用去4.5千克时,用去奶糖多少千克?
【解析:根据水果糖用去的质量算出用去了多少袋,再乘每袋包含奶糖的质量就可以了。】
4.5÷0.15×0.25
=30×0.25
=7.5(千克)
答:(略)
6、姐姐骑电瓶车每小时行18千米,弟弟开小汽车每小时行54千米。他俩从相距247千米的两地同时相向而行,2.5小时后两人还相距多少千米?
247-(18 54)×2.5
=247-72×2.5
=247-180
=67(千米) 答:(略)
以上知识点归纳资料限于篇幅,如需要电子版本,请私信联系。我是梵果教育,关注小学孩子的学习。如果你喜欢我的文章请转发、点赞和收藏,同时我们平台有海量的学习资料及各年级部编版语数英电子课本等,需要的请私信“资料”。,




