如果连续型随机变量的概率密度函数为
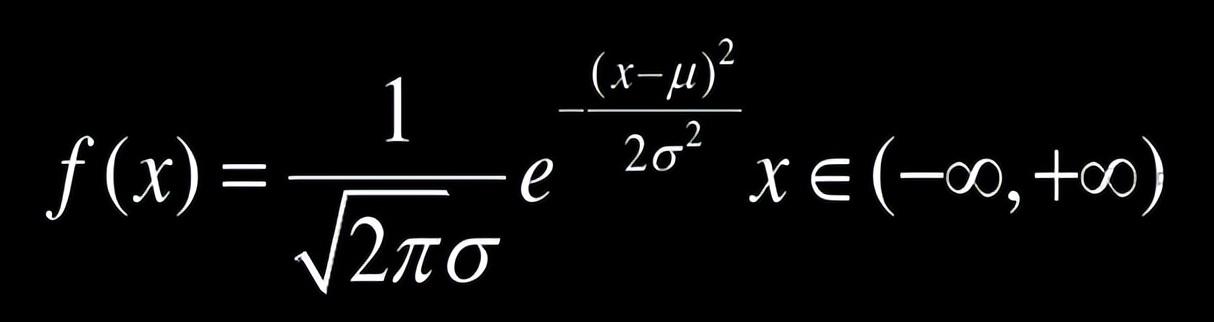
图1

从上面的定义可以看出,正态分布首先是对于连续型随机变量来说的,而学生的分数则应该是离散型随机变量,因为不可能有什么60.1,60.01,60.001分等等。
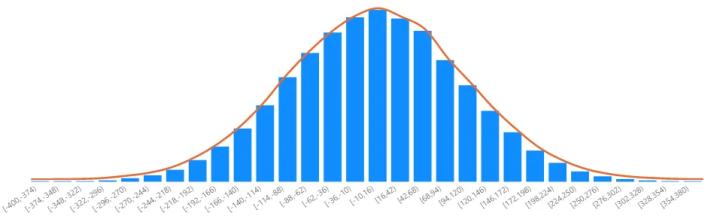
上图是一个正态分布曲线,假设横坐标代表分数,每一个蓝色柱状图和曲线有一个交点,则这个交点的纵坐标就是对应于这个分数的概率密度。但是,假设图中的分数为70,与纵坐标的交点为0.4,那么,“一个班的学生成绩应该服从正态分布”指的是考到70分的学生人数占总人数的40%,即概率的意思。因此:
“一个班的学生成绩应该服从正态分布”,首先这句话等于认为学生的分数是一个连续的实数,而且这个分数的范围是从负无穷到正无穷,这显然是不符合现实的。
其次,对于离散型随机变量来说,只有概率,不存在概率密度的概念,因此,“一个班的学生成绩应该服从正态分布”不但混肴了离散型和连续型随机变量的概念,而且混肴了概率和概率密度的概念。
对于概率密度服从正态分布的随机变量来说,其分布函数是对概率密度函数的积分:


由上图最后一个积分表达式

以及分布函数的定义

可以推导得出正态分布的概率分布函数为

其中

等于1,得到正态分布的分布函数F(x)如下图:

综上所述,学生成绩本来是一个离散型随机变量,但我们套用了连续型随机变量的正态分布概念;同时也混肴了概率和概率密度的含义。但实际工作中,这并不会带来什么太大的影响,只要我们把学生的成绩假想为是整个实数区间就行了。
,




