作者 | 陈关荣(香港城市大学)
来源 | 华院计算

朱莉娅·罗宾逊(Julia Hall Bowman Robinson,1919年12月8日–1985年7月30日)是美国科学院第一位女数学院士和美国数学学会第一位女主席。但是,朱莉娅的遗愿是大家不要去唠叨她是第一位这样或那样的女士,只希望人们知道她的真正身份是一名数学家并记得她留下的数学定理和她解决的数学问题。

【一】
朱莉娅出生于美国密苏里州圣路易斯市。她的父亲拉尔夫·鲍曼(Ralph Bowers Bowman)经营机床设备业务,母亲名叫海伦·霍尔(Helen Hall Bowman)。朱莉娅两岁时母亲因病去世,她和姐姐康斯坦丝(Constance Bowman Reid,1918-2010)被祖母接到了亚利桑那州凤凰城生活。后来,她的父亲与伊登尼亚·克里德堡(Edenia Kridelbaugh)结婚并来到了凤凰城。之后,一家人又搬到了加利福尼亚州圣地亚哥市郊的Point Loma,在那里朱莉娅有了个小妹妹比莉(Billie)。
朱莉娅天生免疫系统不健全,年幼多病。她九岁时染上猩红热,被隔离一年,十岁时又患上风湿热并多次反复,卧床一年。她身体康复后,在一位家教指导下学习了一年,读完了五至八年级的主要课本。老师曾经对她说你无法将2的平方根计算到后面小数可以不断重复的那种程度。这道貌似简单的算术挑战题让她着了迷。她接着进入中学九年级,开始对数学产生极大的兴趣,是选修数学和物理课为数不多的女生之一。1936年,她以优异的数学和科学成绩从中学毕业,获得了全国性的科学全优奖章(Bausch-Lomb medal)。为此,父母亲奖励了她一把计算尺。
接下来,她考进了圣地亚哥州立学院(现在为大学)。当年学院特别重视培养师资,因此她主修数学师资培训课程。期间,她父亲因美国经济大萧条而破产自杀。之后,她凭借姑姑和姐姐的经济支持继续学业。在大学里,她读到了数学家埃里克·贝尔(Eric T. Bell,1883-1960)的名著《数学大师:从芝诺到庞加莱》(Men of Mathematics,1937),被其中的人物、数学特别是数论故事深深吸引。

图2《数学大师》上海科技教育出版社,2012
从《数学大师》一书中朱莉娅明白了师资对知识传承的重要,于是转学到了加州大学伯克利分校继续她的四年级学业,以期修读更好的数学课程。在那里,她选修了助理教授拉斐尔·罗宾逊(Raphael M. Robinson,1911-1995)的数论课程,从中学到了很多有趣的数论知识。她后来愉快地回忆了在伯克利的学生时光:
在伯克利,我很开心,真的很幸福。在圣地亚哥,没有人喜欢我。如果像 Bruno Bettelheim [著名儿童心理学家]所说的每个人都有自己的童话故事的话,那么我的经历就是丑小鸭的故事。在伯克利,我突然发现自己真的是一只小天鹅。有很多人,包括学生和教员,像我一样对数学深感兴趣。我被选为数学联谊会的荣誉成员。我参加了很多社交活动。然后,就是拉斐尔。
1941年底在伯克利研究生第一学期结束后,朱莉娅和拉斐尔结了婚。当年的伯克利分校禁止同一家庭的成员在同一部门任教,因此朱莉娅无法在数学系当助教。她只好把时间花在组建家庭和装修房子上。接踵而来的怀孕让她非常兴奋。然而,她因风湿热导致心脏功能疾病失去了孩子,并且医生建议她不能再要孩子了。这使她伤心至极,接下来经历了一段抑郁期。是拉斐尔重新点燃了她对数学的兴趣,把她从抑郁症中解脱了出来。于是她决定攻读博士学位。在伯克利数学系,她师从著名的波兰裔数理逻辑学家阿尔弗雷德·塔斯基(Alfred Tarski,1901-1983)。这位导师和库尔特·哥德尔(Kurt F. Gödel,1906-1978)是公认的20世纪最重要的两位数理逻辑学家。1948年,她以题为“算术中的可定义性和判决问题”的毕业论文获得博士学位。论文中,她证明了整数在有理数中的可定义性,将哥德尔的“不可判定性”从整数推广到有理数。

【二】
朱莉娅博士毕业之后,随即开始研究希尔伯特第十个问题。
大卫·希尔伯特(David Hilbert,1862-1943)在1900年巴黎举行的第二届国际数学家大会上做了题为“数学问题”的著名演讲,条列了他认为最重要的23个数学问题,其中第十个问题是“丢番图问题”。
丢番图(Diophantus,约200-284)是希腊数学家,他写了一本13卷的著作《算术》(Arithmetica),完整地流传于世的有6卷。丢番图在书中详尽地讨论了各种各样的整系数代数多项式方程,后人称之为丢番图方程。
简单的丢番图方程包括众所周知的方程
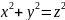
是否有正整数解的问题。大家知道它有解,而且不止一组解,也就是大家熟识的“勾股定理”给出的答案:

以及

,等等。
但出人意料之外,类似的方程
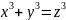
却没有正整数解。1637年,法国业余数学家皮埃尔·德·费马(Pierre de Fermat,1607-1665)在一本小书页边随手写下了一个著名猜想:

在整数

时没有正整数解。这个“费马猜想”到1995年才由英国数学家安德鲁·怀尔斯(Andrew J. Wiles,1953-)和他的学生理查德·泰勒(Richard L. Taylor,1962-)证明是对的。
还有很多形式简单的丢番图方程。一个简单有趣的例子是方程

,其中
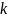
是正整数。一百多年以来,数学家们对

的情形逐个去找它的正整数解。2019年3月,英国布里斯托大学(University of Bristol)的年轻数学家安德鲁·布克(Andrew R. Booker)对

的方程找到了答案。6个月后,布克与麻省理工学院的安德鲁·萨瑟兰(Andrew V. Sutherland)又宣布对

的方程找到了答案。至此,这方程对

时是否有正整数解的问题全部解决了,但人们对更大的的情形依然所知无几。
长期以来,数学家们对丢番图方程是否有整数解的问题都如上述例子那样对特定形式的方程来进行研究,并且通常都希望能够找到解答。希尔伯特对之也颇有期待。但由于很多形式简单的丢番图方程都找不到答案,如上述费马猜想,让人们转而考虑对一般丢番图方程有没有整数解的问题能否找出一种普适算法,来判定“有”或“没有”答案呢?这便是希尔伯特第十问题。这样的问题在数学上称为判定问题,因为它寻求的是对数学命题进行判定的算法。简而言之,希尔伯特第十问题是这样叙述的:“给定一个具有任意有限多个未知数的整数系数的丢番图方程,设计一个算法,使得根据该算法可以通过有限步的操作来确定该方程是否有整数解”。
朱莉娅全力以赴从正面去研究希尔伯特第十问题,梦寐以求能够“找出一种有效的算法来确定任意给定的一个丢番图方程是否可解”。这个问题占据了她后来职业生涯中的绝大部分时间。她是这样的投入,在每年12月8日吹生日蛋糕蜡烛时都默许着同一个愿:希望有一天,她能够知道希尔伯特第十问题的答案。她甚至说:“我无法忍受在不知道答案的情况下离开人世。”

【三】
1950年,朱莉娅在麻省剑桥举行的国际数学家大会上做了一个简短的演讲,报告了她关于希尔伯特第十问题的初步研究成果。在大会上,她认识了刚从普林斯顿获得博士学位的伊利诺伊大学讲师马丁·戴维斯(Martin Davis,1928-),从此两人开始共同探讨丢番图方程问题。马丁后来回忆说,开始时两人的思路是向“绝对相反的方向”发展的。马丁称赞朱莉娅是“非常好的人,非常直截了当。除了数学,她在其他方面还有广泛的兴趣。”
在随后的研究工作中,朱莉娅通过对丢番图方程表示的幂运算和使用佩尔-费马方程的方法形成了一个构想,后人称之为“朱莉娅·罗宾逊猜想”,说是“在一定条件下,存在多项式丢番图方程,其解是指数式增长的函数”。
之后十年时间里,朱莉娅的研究没有太多实质性的进展。
1959年夏天,到了纽约大学任教的马丁和在普林斯顿大学的希拉里·普特南(Hilary Putnam,1926-2016)给朱莉娅寄去了他们的一个密切相关的研究工作结果。三个人详细讨论之后,1961年在《数学年鉴》(Annals of Mathematics)发表了一篇合作论文,其中的主要定理成为后来解决希尔伯特第十问题的重要依据。多年后,马丁回忆说:
她的第一步,几乎就在回信里,说清楚了如何避免混乱的分析。几周后,她展示了如何用算术级数的素数定理代替未经证实的关于素数级数的假设……然后大大地简化了证明。这确实非常巧妙。在发表的版本中,证明是简洁而优雅的。
不过,这还不是问题的最后解答。
十年时间又过去了,他们对最终解决问题的研究依然一筹莫展。
1970 年2月15日,马丁从纽约给朱莉娅打了个电话,说有个同事刚从莫斯科回来,知道列宁格勒(即圣彼得堡)一位22岁的年轻人证明了关系式

(斐波那契数)是满足“朱莉娅·罗宾逊猜想”的丢番图集合。这意味着大多数递归可枚举语言是不可判定的。“这就是我们需要的”,朱莉娅欣喜若狂,“随之而来的是,希尔伯特第十问题的解是否定的——不存在一个判定丢番图方程是否有整数解的一般算法。”
这位22岁的年轻人叫尤里·马季亚谢维奇(Yuri V. Matiyasevich,1947-),当年在列宁格勒的Steklov数学研究所(LOMI)读研究生。
朱莉娅在接到马丁的电话之后,又从另一位在俄罗斯听过该数学证明的计算机科学家朋友手中取得了零碎的笔记。她确认无误之后随即给尤里写了一封信,称赞道:
……现在我知道这是真的。它是美丽的、美妙的。如果你的确是22岁,我特别高兴地想到,当我第一次提出猜想时你还是个婴儿,那时我只需要等着你长大!
当年12月,朱莉娅又去吹生日蛋糕蜡烛了。这次她闭上眼睛,屏住呼吸,开心地想:“突然发现:自己多年的心愿居然实现了”。
马丁也非常激动,他在后来自己的专著《可计算性与不可解性》(Computability and Unsolvability)序言中写道:“ 我一生最大的快乐之一,是 1970年2月看到马季亚谢维奇的工作。”
1971年,朱莉娅和丈夫拉斐尔来到了列宁格勒访问尤里并见到他的妻子物理学家尼娜(Nina)。当时,由于希尔伯特第十问题的解决以及“朱莉娅·罗宾逊猜想”在其中所起的作用,朱莉娅在苏联成为了“罗宾逊漂流记”之后第二个出名的罗宾逊。
从此,数学文献中有了一条著名的Matiyasevich-Robinson-Davis-Putnam定理(简称 MRDP 定理)。先后几个人的共同努力最终解决了希尔伯特第十问题,其答案是否定的:不存在一种普适算法在有限步的操作下能够确定一个丢番图方程是否有整数解。
2008年,《Notices of the AMS》数学杂志对马丁作了一次访谈,其中记者提到:“希尔伯特第十问题通过你们的努力最终解决了,从希拉里·普特南、朱莉娅·罗宾逊、尤里·马季亚谢维奇和你的猜想变成了 DPRM 定理。我们知道在数学领域经常存在优先权的争议,但这好像没有发生在你们四个人身上。”马丁回答说:“的确没有。我们都感到高兴并且互相尊重。我想这是因为我们都很友好!有些人想将结果称为 Matiyasevich 定理,尤里坚持说不,并且说它应该是 DPRM 定理。其他人则把它称为 MRDP 定理。其实我更想讲的一个故事是后来朱莉娅和尤里的进一步合作,他们把方程中的未知数减少到只有9个。”
事实上,尤里在后来一篇文章里写道说:“没有朱莉娅的贡献和启发,我很确定我是绝对不能把

减少到9的。”而朱莉娅在写给尤里的一封信中也说:“我非常高兴地看到,我们(相隔几千里)的合作显然比各自独立研究取得了更大的进展。”朱莉娅毕生把数学看得比个人荣誉更为重要。她说:数学家们应该“像建立自己家园一样,不去区分地域、种族、信仰、性别、年龄,甚至时间(过去的数学家和未来的你都是我们的同事)——全心全意地贡献给这最美丽的艺术和科学。”
最后回来说说尤里的故事,那是颇具戏剧性的。他在上大学时就有兴趣研究丢番图方程,当时自然没啥结果。他后来回忆道:
1969年秋天,一位同事跟我说:“快去图书馆,朱莉娅·罗宾逊在最近一期的美国数学学报上发表了新的论文!”但我早已把希尔伯特第十问题搁置一边了。我对自己说,“朱莉娅·罗宾逊在此问题上取得新进展,这很好,但我不能再花时间在这个问题上了”。因此,我没有去图书馆。但一定是在数学天堂的某个地方,有一位数学之神或女神,指引我不要错过朱莉娅·罗宾逊的新论文。由于我早期在此领域上发表过论文,算是个专家,因此《数学评论》苏联版给我邮寄来了她的论文,让我写个评论。这样,我在毫无打算的情况下阅读了朱莉娅·罗宾逊的文章,并于12月在 LOMI 的逻辑研讨会上介绍了她的论文。希尔伯特第十问题再次吸引了我,并且我立即注意到了朱莉娅·罗宾逊提出的一种新颖方法。
尤里仔细研究了那篇只有5页的论文,内容是关于两个变量中某些丢番图方程解的相对增长问题。论文中的思想启发他完成了最终证明。尤里的论文通过了著名数学家德米特里·法迪耶夫(Dmitrii K. Faddeev, 1907-1989)和安德烈·马尔科夫(Andrey A. Markov, 1903-1979)的严格审查。1970年,尤里在法国 Nice 举行的国际数学家大会上宣讲了他的结果。
多年以后,1993年尤里在《数学信使》(The Mathematical Intelligencer)的一篇概述性科普文章中说:“事实上,朱莉娅当时已经非常接近希尔伯特第十问题不可解性的完全证明了。”尤里的主要贡献是巧妙地构造了一个具体的例子验证了“朱莉娅·罗宾逊猜想”的条件,让她的猜想变成了定理。尤里数学证明的理论和技术难度也许算不得非常高深,正如多年后朱莉娅在自传中不经意地说的那样:“他的证明没有什么东西是在初等数论课程里面找不到的!”无论如何,尤里“临门一脚”是不可或缺的。同时,数学界普遍认为,朱莉娅·罗宾逊的名字和希尔伯特第十问题是绝对分不开的。
作为后话,1972年尤里以该成果获得苏联国家博士学位,1980年获苏联科学院马尔可夫奖,1996年获法国奥弗涅大学大学(l'Université d'Auvergne)荣誉博士学位,1997年当选为俄罗斯科学院通讯院士,2003年获法国巴黎皮埃尔和玛丽居里大学(l'Université Pierre et Marie Curie in Paris)荣誉博士学位,2008年当选为俄罗斯科学院院士。

图5 马丁、朱莉娅和尤里
希尔伯特第十问题解决之后,数学家们进一步考虑:如果改变丢番图方程解的类型将会如何?一种很自然的改变或推广就是将问题转向有理数:有没有一种普适算法可以确定一个有整数系数的多项式方程存在有理数解?对于这个问题,数学家们一般认为答案依然是否定的,不过他们离给出严格证明还有很长的路程要走。有人认为,解决这个问题的一个可能途径估计还得回到朱莉娅·罗宾逊70多年前的博士论文去。
【四】
尽管朱莉娅把大部分时间都花在希尔伯特第十问题上,她也做了一些其他研究和管理工作。1949年,她毕业后到了加利福尼亚州兰德公司(RAND Corporation)工作,在那里她研究零和博弈理论。她在一篇技术报告“关于哈密顿图游戏(一个旅行推销员问题)”里第一次使用了“旅行推销员问题”的称谓。1951年,她发表论文“解决游戏的迭代方法”,证明了虚拟游戏动力学收敛于两人零和博弈中的混合策略纳什均衡。这段时间里,朱莉娅也参与斯坦福大学为海军研究办公室(Office of Naval Research)做的流体动力学科研项目。在1952年和1956年,她参与了阿德莱·史蒂文森(Adlai E. Stevenson,1835-1914)的总统竞选活动,并在随后的六年里为民主党做社会工作。
由于对解决希尔伯特第十问题的贡献,1975年朱莉娅当选为美国科学院院士,成为美国历史上第一位女数学院士。翌年,她在伯克利获聘为全职正教授,那是她1949年获得博士学位以来的第一份正式教职。但是,由于健康原因,她只承担了四分之一的教学任务。1979年,她获 Smaith College 授予荣誉学位。1982年,她当选为美国数学学会主席,成为该学会历史上第一位女主席。同年,她还获得 MacArthur Foundation 奖以及女数学家协会颁发的诺特(Noether)奖,并在该奖名义下举办了“算术函数方程”系列讲座。1985年,她又被遴选为美国国家艺术与科学院院士,并被列入美国100位最杰出女士名人录。
关于担任数学学会主席的职务,朱莉娅在自传中留下了这么一段话:
作为一个女性和一个数学家,我别无选择,只能接受,尽管我一直竭尽所能去鼓励有才华的女性成为研究型数学家。我发现我担当学会主席的工作很累,但同时也令自己感到非常、非常愉快。

图6 朱莉娅院士、美国数学学会主席
【五】
1941年朱莉娅因心脏疾病失去胎儿时,医生告诉她母亲说如果朱莉娅能活到40岁就很幸运了。事实上,到了1961年朱莉娅41岁时,她的心脏疾病重发,需要动手术除去积聚在心脏里的坏死疤痕组织。幸亏手术成功,随后她的健康状况日渐改善。一个月后,她就可以骑自行车去锻炼身体了。后来,她锻炼上了瘾,先后买了六辆运动自行车,在美国甚至到荷兰旅行时骑自行车作长途旅行。她丈夫拉斐尔有点无奈地开玩笑说:“别人的妻子买皮大衣和钻石手镯,而我的妻子买自行车。”
1984年夏天,朱莉娅不幸患上了白血病,于1985年7月30日在加利福尼亚州奥克兰去世,享年66岁。
根据朱莉娅的遗愿,学校和学会都没有举办葬礼。她去世前留下建议,希望那些为纪念她作捐赠的朋友可以把款项转送给由伯克利数学系代管、为纪念她的导师而设立的 Alfred Tarski 基金。
为了纪念她,1996年美国数学学会出版了她的论文集。2013年开始,美国数学学会设立并赞助了每年12月举行的“朱莉娅·罗宾逊数学节”。导演 George Csicsery 还制作了一部题为“朱莉娅·罗宾逊和希尔伯特第十个问题”的纪录片,于2008年1月7日在圣地亚哥举行的美国数学学会和美国数学协会的联合会议上首映。
当朱莉娅知道自己患上不治之症时,请姐姐康斯坦丝为她写下一些人生回忆录。姐姐是个数学科普及传记作家,几周后就写好了简要的“朱莉娅·罗宾逊自传”(The Autobiography of Julia Robinson)。多年后,她又出版了详细的传记《朱莉娅:数学人生》(“Julia:ALife in Mathematics”,MAA Press,1996)。
“我的真正身份是一名数学家”,姐姐在书末忆述了朱莉娅临终前的一段话,“与其作为第一个这样或那样的女士被人记住,我更愿意自己像一位数学家应该的那样,是因为证明了的定理和解决了的问题而被人们记住。”

图7朱莉娅和姐姐康斯坦丝






