点击右上角关注“陈老师初中数理化”分享学习经验,一起畅游快乐的学习生活。
利用菱形和切线性质求解与菱形相切的圆半径是数学中考的常考题型,本文就例题详细解析这类题型的解题方法,希望能给初三学生的数学复习带来帮助。
例题如图,菱形ABCD的边AB=20,面积为320,∠BCD<90°,⊙O与边AB,AD都相切,AO=10,求⊙O的半径。
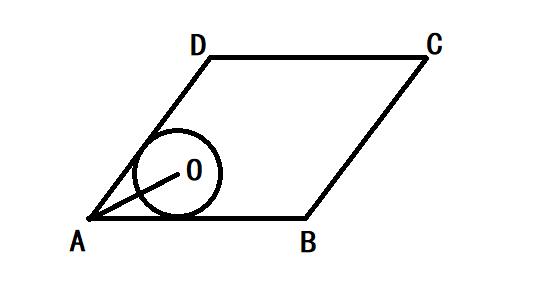
解题过程:
设⊙O与AB、AD的切点为E、F,连接OE、OF、AC、BD,设AC、BD的交点为M

根据切线的性质和题目中的条件:⊙O与AB、AD的切点为E、F,则OE⊥AB,OF⊥AD;
根据角平分线判定和结论:OE⊥AB,OF⊥AD,OE=OF,则AO为∠BAD的平分线;
根据菱形的性质和题目中的条件:四边形ABCD为菱形,则AC为∠BAD的平分线,AC⊥BD,AC=2AM,BD=2BM;
根据结论:AO为∠BAD的平分线,AC为∠BAD的平分线,则A,O,C三点在一条线上;
根据结论:OE⊥AB,AC⊥BD,则∠AEO=∠AMB=90°;
根据相似三角形的判定和结论:∠AEO=∠AMB,∠OAE=∠BAM,则△AOE∽△ABM;
根据相似三角形的性质和结论:△AOE∽△ABM,则OE/AO=BM/AB;
设BM=x,AM=y
根据结论:BM=x,AM=y,AC=2AM,BD=2BM,则AC=2y,BD=2x;
根据勾股定理和结论:AC⊥BD,BM=x,AM=y,AB=20,则AB^2=BM^ AM^2,即x^2 y^2=400;
根据菱形的面积公式和结论:AC=2y,BD=2x,S菱形ABCD=AC*BD/2=320,则xy=160;
根据结论:x^2 y^2=400,xy=160,x<y,则x=4√5,y=8√5,即BM=4√5,AM=8√5;
根据题目中的条件和结论:OE/AO=BM/AB,BM=4√5,AO=10,AB=20,则OE=2√5;
所以,⊙O的半径为2√5。
结语解决本题的关键是根据菱形的对角线互相垂直平分、平分对角的性质,添加辅助线构造出一组相似的直角三角形,利用菱形面积公式和勾股定理,得到一个用菱形的对角线表示的二元一次方程组,再利用相似三角形对应边成比例的性质就可以求得圆的半径。
,




