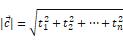向量是一个有大小也有方向的量,我们用粗体或带箭头的量表示一个向量,例如a。只有大小没有方向的量,我们称之为标量。
向量与坐标的联系一个点的坐标在平面直角坐标系中是标量,是一个绝对的位置,坐标系确定了之后,它的位置就不再发生变化,用坐标(x, y)可以表示一个点的位置。从另一个角度理解,可以将坐标看作为起始点为原点(0, 0)的向量终点位置。之所以将一个点的坐标看作一个绝对位置,那是因为原点的位置是固定的。一个点与另一个起始点的相对位置就可以用向量表示,点A(x, y) 相对于B(m, n)的位置,那么可以用下面的等式表示

两个坐标的差值就代表一个向量

(m, n)是起始点,起始点发生变化,这个点的相对坐标就发生变化了,向量就发生变化。如果起始点在原点处,那么坐标也可以表示这个点相对于原点的向量,向量(x, y)表示从原点指向点(x, y)。

在平面直角坐标系中可以用二维坐标代表平面向量。同样的道理,在空间坐标系中,可以用三维坐标表示空间向量。因此向量与坐标一样,都是有维度的。更一般地,可以用n个数字表示n个维度的坐标和向量。
向量的大小表示向量在平面直角坐标系中的意义,就是从一个点按照直线平移到另一个点,那么其平移的最短路径就是向量的大小,称之为向量的模。用勾股定理可知,向量a=(x, y)的模为
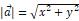
在三维空间中,向量b=(x,y,z)的模为

那么扩展到n维空间,向量c=(t1,t2,…,tn),它的模为