在几个物体保持相对静止时,往往会用整体法,实际上几个物体相对运动时也可以用整体法,称为系统牛顿第二定律。

两个物体组成一个系统,外界对系统内物体有力的作用(系统外力),系统内物体之间也有相互作用力(内力)
粗体表示矢量
对1:F₁ F₂₁=m₁a₁
对2:F₂ F₁₂=m₂a₂
其中,F₂₁=-F₁₂
通过牛顿第三定律把内力抵消
联立得:F₁ F₂=m₁a₁ m₂a₂
这就是系统牛顿第二定律,可以推广到多个物体。

正交分解形式:

☞整体法的优点是无需考虑内力,如果要求内力,必须用隔离法。
☞若用系统动能定理,需要考虑内力的功,内力的功之和不一定为零。
一、两静型
例:在粗糙的水平面上有一三角形木块A,A的两个粗糙斜面上分别放着B、C两个小木块,如图所示。

已知A、B、C三木块都静止,则粗糙水平面对三角形木块(C、F)
A.有摩擦力的作用,摩擦力的方向水平向右
B.有摩擦力的作用,摩擦力的方向水平向左
C.没摩擦力的作用
D.有摩擦力的作用,但摩擦力的方向不能确定,因为A、B质量和斜面的倾角未给出
E.水平面对三角形木块的支持力大于三个物体的重力之和
F.水平面对三角形木块的支持力等于三个物体的重力之和
二、一静一动型
例:如图所示,

在粗糙水平面上放一三角形木块a,物块b在a的斜面上匀速下滑,则(A)
A.a保持静止,而且没有相对于水平面运动的趋势
B.a保持静止,但有相对于水平面向右运动的趋势
C.a保持静止,但有相对于水平面向左运动的趋势
D.因未给出所需数据,无法对a是否运动或有无运动趋势作出判断
例:如图所示,

质量M=10kg的木楔ABC静置于粗糙水平地面上,动摩擦因数μ=0.02。在木楔的倾角θ=30°的斜面上,有一质量m=1.0kg的物块由静止开始沿斜面下滑,当滑行路程s=1.4m时,其速度v=1.4m/s,在这过程中木楔没有动。求地面对木楔的支持力和摩擦力。(重力加速度取g=10m/s²)
例:质量m=5kg的物体,置于质量M=20kg,倾角α=30°的粗糙斜面上,斜面放在粗糙水平地面上,如图所示。

现用平行于斜面、大小为F=30N的力推物体,使物体沿斜面匀速上行。在这过程中,斜面体与地面保持相对静止。求地面对斜面体的摩擦力和支持力的大小。取g=10m/s²。
例:如图所示,

质量为M的木板可以沿倾角为θ(θ较小)的斜面无摩擦地滑下。欲使木板静止,质量为m的人应在这木板上以多大的加速度向哪方向运动?
例:如图所示,
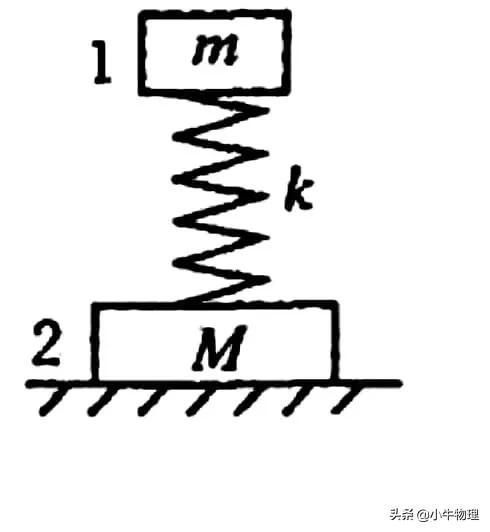
两木块质量分别为m和M,用劲度系数为k的轻弹簧连在一起,放在水平地面上,将木块1压下一段距离后释放,它就上下作简谐振动。在振动过程中木块2刚好始终不离开地面(即它对地面最小压力为零)。则:
(1)木块1的最大加速度大小是多少?
(2)木块2对地面的最大压力大小
例:如图所示,
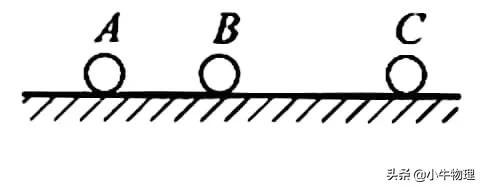
在光滑水平面上固定三个等质量的带电小球(均可视为质点)A,B,C,三球排成一直线.若释放A球(另两球仍固定)的瞬时,A球的加速度大小为1m/s²,方向向左;若释放C球(另两球仍固定)的瞬时,C球的加速度大小为2m/s²,方向向右;则释放B的瞬时,B球的加速度大小为___m/s²,方向___。
例:如图所示,

一质量为M的楔形木块放在水平桌面上,它的顶角为90°,两底角为α和β;a、b为两个位于斜面上质量均为m的小木块,已知所有接触面都是光滑的。现发现a、b沿斜面下滑,而楔形木块静止不动,这时楔形木块对水平桌面的压力等于()
A.Mg+mg
B.Mg+2mg
C.Mg+mg (sinα+sinβ)
D.Mg+mg (cosα+cosβ)
三、两动型
例:如图所示,

在水平面上有一质量为M的楔形木块A,其斜面倾角为α,一质量为m的木块B放在A的斜面上,现对A施以水平推力F,恰使B与A不发生相对滑动,忽略一切摩擦,则B对A的压力大小为___。
例:如图所示,
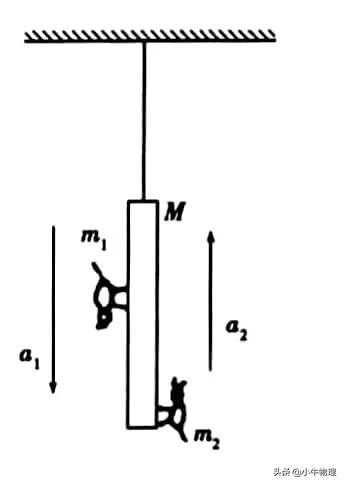
用细绳竖直悬挂一质量为M的木杆,杆的上、下两端各有质量分别为m₁、m₂的小猫,若质量为m₁的小猫以加速度a₁加速下滑,质量为m₂的小猫以加速度a₂上爬,求悬绳中的张力。
例:如图所示,

质量为m的小物体自高度为h、倾角为θ、质量为M的斜面的顶端以零初速滑下,当小物体滑到斜面底端时它相对于地面的速度刚好沿水平方向并设所有的接触面都光滑,求:
(1)斜面M在水平面上移动的距离;
(2)小物体滑到斜面底端时其相对于斜面的速度。
例:如图所示,

轻杆的两端分别固定两个质量均为m的小球A、B,轻杆可以绕距A端1/3杆长处的固定转轴O无摩擦地转动.若轻杆自水平位置由静止开始自由绕O轴转到竖直状态时,求转轴O对杆的作用力.

,




