一、有关力的问题
例题:如图所示,

将一根不可伸长、柔软的轻绳左、右两端分别系于A、B两点上,一物体用动滑轮悬挂在轻绳上,达到平衡时,两段绳子间的夹角为θ₁,绳子张力为F₁;将绳子右端移到C点,待系统达到平衡时,两段绳子间的夹角为θ₂,绳子张力为F₂;将绳子右端再由C点移到D点,待系统达到平衡时,两段绳子间的夹角为θ₃,绳子张力为F₃,不计摩擦,并且BC为竖直线,则(AD)
A.θ₁=θ₂<θ₃
B.θ₁=θ₂=θ₃
C.F₁>F₂>F₃
D.F₁=F₂>F₃
例题:如图所示,
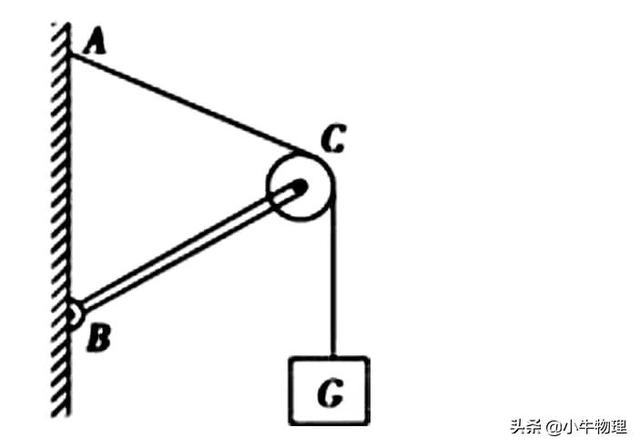
杆BC的B端用铰链接在竖直墙上,另一端C为一滑轮.重物G上系一绳经过滑轮固定于墙上A点处,杆恰好平衡.若将绳的A端沿墙缓慢向下移(BC杆、滑轮、绳的质量及摩擦均不计),则(B)
A.绳的拉力增大,BC杆受绳的压力增大
B.绳的拉力不变,BC杆受绳的压力增大
C.绳的拉力不变,BC杆受绳的压力减小
D.绳的拉力不变,BC杆受绳的压力不变
例题:北京残奥会开幕式上,运动员手拉绳索向上攀登,最终点燃了主火炬,体现了残疾运动员坚韧不拔的意志和自强不息的精神.为了探求上升过程中运动员与绳索和吊椅间的作用,可将过程简化为一根不可伸缩的轻绳跨过轻质的定滑轮,一端挂一吊椅,另一端被坐在吊椅上的运动员拉住,如图所示.

设运动员的质量为65kg,吊椅的质量为15kg,不计定滑轮与绳子间的摩擦,重力加速度g取10m/s².当运动员与吊椅一起以加速度a=1m/s²上升时,试求:
(1)运动员竖直向下拉绳的力;
(2)运动员对吊椅的压力.

二、有关加速度的问题
例题:如图甲所示,滑轮质量、摩擦均不计,质量为2kg的物体在F作用下由静止开始向上做匀加速运动,其速度随时间的变化关系如图乙所示,由此可知(取g=10m/s²)()

A.物体加速度大小为2m/s²
B.F的大小为21N
C.4s末F的功率大小为42W
D.4s内F做功的平均功率为42W

☞力F作用点的速度是物体速度的2倍,力F作用点的加速度是物体加速度的2倍.
三、有关关联速度问题
例题:如图所示,

重物M沿竖直杆下滑,并通过绳带动小车沿斜面升高。问:当滑轮右侧的绳与竖直方向成θ角,且重物下滑的速率为v时,小车的速度为()
A.vsinθ
B.v/cosθ
C.vcosθ
D.v/sinθ
例题:如图所示,

小车匀速向右运动,不计绳子的质量和一切摩擦阻力,物体A的受力情况是(A)
A.绳子的拉力大于A的重力
B.绳子的拉力小于A的币力
C.绳子的拉力等于A的重力
D.拉力先是大于重力,后变为小于重力
四、有关关联加速度问题
例题:如图所示,

一轻绳通过一光滑定滑轮,两端各系一质量分别为m₁和m₂的物体,m₁放在地面上,当m₂的质量发生变化时,m₁的加速度a的大小与m₂的关系图象大体如下图中的()


☞在不涉及转动问题时,绳子两端物体加速度大小是相等的.
五、有关功和能的问题
例题:如图所示,

物块右端有一个质量不计的滑轮,细绳的一端系在墙上B点,另一端绕过滑轮受到恒力F的作用,力F跟水平面夹角为θ,跟B点相连的细绳处于水平位置。在力F作用下,物块沿水平方向移动S的过程中,恒力F做的功为?

例题:如图所示,

细绳绕过两个定滑轮A和B,在两端各挂一个重为P的物体,现在A、B的中点C处挂一个重为Q的小球,Q<2P,求小球可能下降的最大距离h.已知AB长为2L,不计滑轮和绳之间的摩擦力及绳的质量.






