什么样的数列收敛（大自然的鬼斧神工）

我们继续聊级数，这次我们的主角是：

我们上次讲到了发散和收敛，那这个级数究竟是发散的还是收敛的呢？

你一看，我的老天，这也太难了吧，我根本看不懂。

莫慌，我们还是用老办法，一步一步来分析：

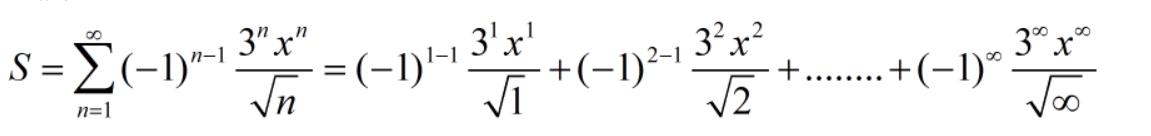
我们化简一下，可以得到：

我们展开上面那个通式后，发现依然毫无头绪，在这个异常复杂的数学表达式里，它究竟蕴含着怎样的秘密呢？

于是，我们需要理所应当地引入一些数学工具了：

首先，为了简化上面那个级数的研究内容，我们定义出一些新的东西来方便描述它：

An的意思是“数列”，它把这个复杂的东西包括进去了

我们姑且把这个称为交错因子

这个交错因子有什么用呢？我给大家举个例子：

我们引入收敛域和收敛半径的概念：

什么是收敛域呢？举个例子，你就明白了：

我们代-1到1之间的所有实数用可以使得上式成立，可是你假如超过了上面这个范围就不成立了：

我们就把(-1,1)称为上面这个级数的收敛域

上面的级数只有在这个范围内才是收敛的

那收敛半径R又是什么呢？

关于收敛半径R，大家先简单理解为收敛域的左右端点值（正的那个1）。

怎么求这个收敛半径呢，今天我只请出大数学家达朗贝尔来描述这个问题。

达朗贝尔（1717～1783），法国数学家，哲学家。1717 年11月 17 日生于巴黎，1783年10月29日卒于同地。他是圣让勒隆教堂附近的一个弃婴 ，被一位玻璃匠收养，后来这个教堂的名字就成了他的教名 。达朗贝尔在数学、力学和天文学等许多领域都作出了巨大的贡献。————百度百科

达朗贝尔说道，我有一个定理，能帮你求出收敛半径：

达朗贝尔定理

于是，我们用上这个公式，进行计算：

收敛半径R:

我们现在得到了收敛域（-1/3,1/3), 你说道——这就是收敛域！

然而，莱布尼兹又出来说话了：我们必须考虑临界的端点位置，数学是严谨的，你这个收敛域很可能缺少了东西。

既然如此，我们不得不带进去看一下实际情况。当x=-1/3时：

这个级数是发散的，所以不能取端点。

而

我们莱布尼兹交错级数判别法：

则在这一点是收敛的。

所以，我们得到了真正的收敛域:

,