很多同学碰到函数题都很茫然,各种函数傻傻分不清。有的题目要求对函数图像进行各种变换,更是让同学们摸不清头脑。小编今天就把高中数学里用到的函数都整理出来给大家,图文并茂,非常便于记忆哦!
一、基本初等函数的图像基本的函数图像是同学们必须记清楚的,只有记清楚了基本的函数图像,才能应对各种变换要求。
跟小编一起来看看,下面这些基本的函数图像你都记清楚了没!
1一次函数
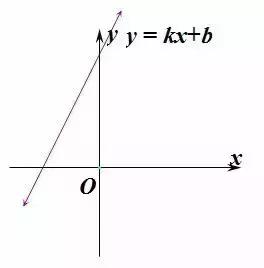
性质:一次函数图像是直线。当k>0时,函数单调递增;当k<0时,函数单调递减。
2二次函数

性质:二次函数图像是抛物线。a决定函数图像的开口方向,判别式b^2-4ac决定了函数图像与x轴的交点,对称轴两边函数的单调性不同。
性质:反比例函数图像是双曲线。当k>0时,图像经过一、三象限;当k<0时,图像经过二、四象限。要注意表述函数单调性时,不能说在定义域上单调,而应该说在(-∞,0),(0,∞)上单调。
4指数函数

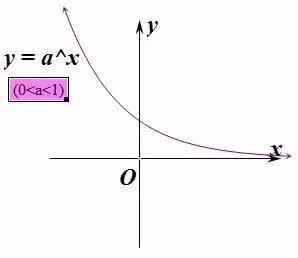
当0<a<b<1<c<d时,指数函数的图像如下图

不同底的指数函数图像在同一个坐标系中时,一般可以做直线 x = 1,与各函数的交点,根据交点纵坐标的大小,即可比较底数的大小。
5对数函数

当底数不同时,对数函数的图像是这样变换的

6幂函数
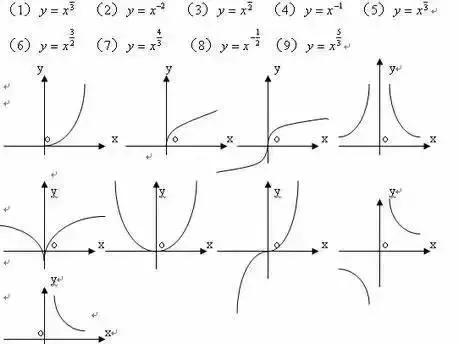
性质:先看第一象限,即x>0时,当a>1时,函数越增越快;当0<a<1时,函数越增越慢;当a<0时,函数单调递减;然后当x<0时,根据函数的定义域与奇偶性判断函数图像即可。
7对勾函数

对于函数y=x k/x,当k>0时,才是对勾函数,可以利用均值定理找到函数的最值。
二、函数图像的变换1平移变换
(1)水平平移:函数 y = f(x a)的图像可以把函数 y = f(x)的图像沿x轴方向向左(a>0)或向右(a<0)平移|a|个单位即可得到;
(2)竖直平移:函数 y = f(x) a 的图像可以把函数 y = f(x)的图像沿x轴方向向上(a>0)或向下(a<0)平移|a|个单位即可得到。
2对称变换
(1)函数 y = f(-x) 的图像可以将函数 y = f(x)的图像关于y轴对称即可得到;
(2)函数 y = - f(x) 的图像可以将函数 y = f(x)的图像关于x轴对称即可得到;
(3)函数 y = - f(-x) 的图像可以将函数 y = f(x)的图像关于原点对称即可得到;
3翻折变换
(1)函数 y =| f(x)| 的图像可以将函数 y = f(x)的图像的x轴下方部分沿x轴翻折到x轴上方,去掉x轴下方部分,并保留 y = f(x)的x轴上方部分即可得到;
(2)函数 y = f(|x|) 的图像可以将函数 y = f(x)的图像的右边沿y轴翻折到y轴左边替代原y轴左边部分并保留 y = f(x)在y轴右边部分即可得到。
4伸缩变换
(1)函数 y = a f(x) (a>0)的图像可以将函数 y = f(x)的图像中的每一点横坐标不变,纵坐标伸长(a>1)或压缩(0<a<1)为原来的a倍得到;
(2)函数 y = f(ax) (a>0)的图像可以将函数 y = f(x)的图像中的每一点纵坐标不变,横坐标压缩(a>1)或伸长(0<a<1)为原来的1/a倍得到;
注意:对于函数图像的变换,有的时候,看到解析式,可能会有两种以上的变换,尤其是针对x轴上的,那么此时,一定要根据上面的规则,判断好顺序,否则顺序错了,可能就没办法经过变换得到了!
三、小试牛刀练一练小编已经总结了基本函数的图像以及图像变换的一些步骤,下面我们就来练一练!
练一练:画出函数 y = ln|2-x|的图像
通过研究这个函数解析式,我们可以知道此函数是由基本初等函数 y = lnx通过变换而来,那么这个函数经过了几步变换呢?变换的顺序又是如何?下面我们一起来看一看!
通过解析式x上附加的东西,我们会发现,会有对称变换,x前面加了负号,还有翻折变换,x上面还有绝对值,还有平移变换,前面加了一个2,既然有3种变换,那么顺序如何呢?牢记住一点:针对x轴上的变换,那就一定要看x这个符号有啥变化。
所以,我们可以得出:第一步,翻折变换;第二步,对称变换;第三步,平移变换。
有的同学说,第一步是对称变换,也就是先在x上加负号,但是接下来的话,再进行翻折变换,就相当于在-x上加绝对值了,而这个并不是我们学过的规律,所以后面就无法进行变换了,这样也就错了。同学们一定要切记哈!
当然,如果同学们能对这四种变换很熟悉的话,那就可以先对解析式进行变形,化为 y = ln|x-2|,这样只经过两步变换即可了!
第一步:先画出函数 y = lnx的图像
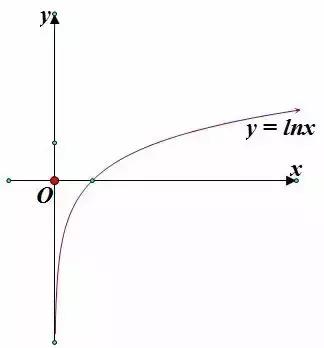
第二步:进行翻折变换,得到函数 y = ln|x|的图像
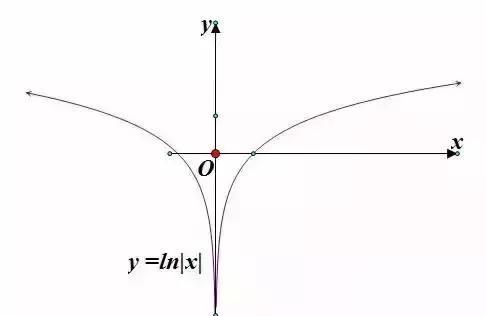
第三步:进行对称变换,得到函数 y = ln|-x|的图像

第四步:进行平移变换,得到函数 y = ln|2-x|的图像

*来源:整合自网络
,




