
几乎我们每个人都喜欢气球,在婚礼、庆典和开幕式等重要场合上,都会伴有它的身影。而对年幼的孩童们更是如此,孩子们(通过他们的观察)正在慢慢地建立关于这一星球上基本物理定律的观念,他们已经知道当我们放手某样东西时,它就会掉下来。不过,一个充满氦气的气球打破了这一固有"常规"。它会上升——直至飘到
看不见的地方,这对于年幼时期的我们也是一件极为神奇的事情,那个时候的我们可能会常常幻想:在自己身上绑着很多气球,也可以一样飘上高空中。
对于这一个奇幻的儿时幻想,我们每个人都在某些时候考虑过这个问题: 到底需要多少个这样的气球才能让我们飞离地面?首先,肯定的答案是:只要气球数量足够,我们肯定可以被气球带上空中。就在上周9月2日,我们的这一梦想被美国魔术师大卫·布莱恩(David Blaine)给实现了。他抓着52个氦气气球成功地将自己升到7315.2米(24000英尺)高度的高空中,这时,他脱开绳索将自己从气球中分离出来,用降落伞安全回到了地面。他将此次飞行特技表演为"跃升"。

在笔者看来,这个飞行特技表演最精彩的部分是最初的发射阶段。该表演的幕后团队通过对于气球的精确计算——使气球产生的浮力和把布莱恩拉下来的重力之间有一个近乎完美的平衡,因此布莱恩 (Blaine)大部分时间都只是漂浮在地上。(从视频中可以看出,他确实让一些人紧紧抓着他,以确保他不会过早地飘浮离开)。然后,为了让他开始上升的旅程,他的女儿又加了一个气球,他把自己一直拿着的一个重物交给了她。随后就开始了他的奇妙"跃升"之旅。
那么,接下来开始我们的好奇探究之旅——大致分析和计算一下,到底要多少气球才可以让大卫·布莱恩升空?

当然,气球肯定不是靠魔法飘起来的。而是因为其受到重力和大气层的影响。对,这是真的。如果没有重力,气球是不会飘起来的。
让我们把大气层想象成一堆球——只不过这些球实际上是主要由氮气和一些氧气组成的分子。每一个球都以一定的平均速度运动,它们因与地球的引力相互作用而被下拉。所以,我们可以把这些"气"球想象成一个网球扔在房间里,只是它们非常小。哦,不单只有一个球,而是一堆被扔进这个房间。这就意味着它们会与其他球相互作用,我们可以把这些相互作用看作是碰撞。正是这些球与球的碰撞,才使它们不至于就这样落在地上。另外,如果所有的空气都聚集在最底层,那将会产生非常尴尬的现象,因为那样我们就无法呼吸了。

当两个"气"球相撞时,有时其中一个球会向上偏转,有时也会向侧向偏转。然而,由于还存在着引力作用会将这些球拉下来,所以有更多的球靠近地面。这就是为什么当火箭垂直向上移动时,会发现空气的密度逐渐降低。靠近地面的空气密度约为1.2千克/立方米,在海拔高达7000米时,空气密度会降低到0.59千克/立方米左右。但即使是从气球(自然垂直的情况下)底部到顶部的小距离内,空气的密度也会发生变化——只不过这一变化微乎其微。
现在让我们把一个物体放到空中。比如,一块砖头,它是一个很好的例子。因为它显然不会漂浮在空中,而且它还有平坦的表面,这样更有利于我们解释和理解。因为这些微小的"气"球在周围运动,所以其中一些会与砖块的表面发生相撞。当一个球从砖块上反弹时,它会给砖块一个微小的推力。砖块的一个表面上所受的总力,取决于该块砖的面积和空气的压力。

注释:力和压力的关系可以用上图的公式表示,其中P是压力,A是面积,F是力。
所以,如果你有一个很大的表面积,即使在压力很小的情况下,你仍然可以得到一个很大的力。在这个表达式中,压力是由于大气层造成的——也就是大气中的这些球在周围移动并与物体碰撞而致。不过,在这里有一个很有趣的部分。因为离地面较近的"气"球较多,所以压力可视为取决于空气的密度,并且记住,密度取决于海拔高度。这就意味着,空气对砖块顶部的作用力与砖块底部的作用力是不同的。所以,最好用压强来描述这些碰撞,并用下面的公式来模拟压力的变化。

在这个表达式中,P0是某一任意点的压力,其中y=0(垂直方向上);g是重力加速度(9.8 N/kg);ρ是空气的密度。所以随着y的增加,压力会减小。注意:这种线性关系只是近似正确的。当你离地球表面非常远的时候,其就无法适用了。但是通过该公式,我们可以看到空气对砖头顶部的作用力,应该是小于砖头底部的作用力。

其中应注意的是,推动砖块左右两侧的力是处于同一高度。这就意味着水平方向上的合力将为零——两者抵消。但由于砖的底部处于较低的高度,所以向上推的作用力(从底部)将会大于向下推的作用力——即使只有一点点。如果砖块的高度为h,那么来自空气在垂直方向的总力为:
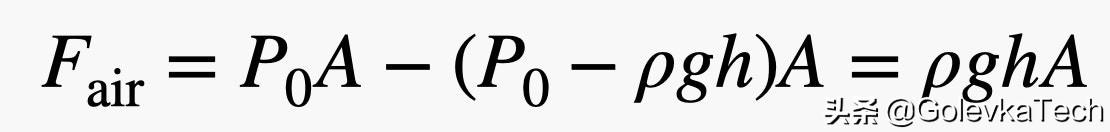
请注意,在这里跳过了一些代数步骤,但这并不难看出是如何解决的。如果我们用砖的高度(h)乘以底部的面积(A),将会得到砖的体积(V)。然后,再用砖的体积乘以空气的密度(ρ),就可以得到一个质量——与砖的体积相同的空气质量。当你把这个质量和重力加速度(g)相乘时,我们就会得到被砖块置换的空气重量。
嗯没错,这就是著名的阿基米德原理:当一个物体在水中时,物体上有一个向上的浮力。这个浮力的值等于排开水的重量。同样,它也适用于被置换的空气。是的,砖头上有一个向上的空气浮力。只不过砖头不会像气球一样漂浮,因为砖头上还有一个向下的重力——这个向下的重力要远比向上的浮力大得多。
那么,我们开始进入正题。如果你把矩形的砖块换成球形的气球也是同理。浮力仍然只是取决于空气的密度和物体的体积。那么,氦气球为什么能浮起来呢?氦气唯一特殊的地方就是它的密度比空气低得多(氦气的密度为0.179千克/立方米,空气的密度为1.2千克/立方米)。这意味着,向下拉气球的重力小于向上的浮力,气球就会漂浮起来。要清楚一点是,一个装满水的气球和一个同样大小的氦气球的浮力是一样的。只是装满水气球的重量很大。

这里并不是指我们应该亲身去做试验,用一堆气球将自己漂浮到空中。我们只是假设估算一下一个人漂浮所需的气球数量。与上文同理,要计算出与人体重相等的空气体积,然后计算出你需要的氦气的体积,这并不太难。但是这忽略了一些非常重要的东西——气球中的橡胶。是的,虽然它的质量很小,但当它达到一定数量后就并非可忽略不计了。假设我们有一个由任意厚度的橡胶制成的普通球形气球。也许它看起来像下图这样。

这个气球的半径为R,橡胶厚度为t,里面充满了氦气。下一步,则需要求出氦气和橡胶的质量(也就是重量)。在公式中,氦气的密度为ρh,橡胶的密度为ρr。氦气的重量取决于气球的体积。因为它可近似是一个球体,所以氦气的重量将是:

在这里所使用的球体体积公式,只是进行了理想化的近似计算。现在让我们来看看橡胶的重量计算。首先我们需要气球外面这个薄壳的体积。如果橡胶的厚度与气球的半径相比较小(这是近似的),那么我们可以计算橡胶的体积作为球体的表面积乘以厚度。这样就得到了橡胶的重量为:

橡胶的重量中有一个参数t(气球中橡胶厚度)。简而言之,我们不能把气球做得越薄越好。我们假设一个限定条件:我们将t值视为一个恒定值。这就意味着,橡胶的重量与气球半径的平方成正比,而氦气的重量与半径的立方成正比。氦气的密度比橡胶低得多,所以需要一个较大的氦气和橡胶的比例值(氦橡胶比),这意味着气球越大越好。
如果从派对中常用的气球来看,它有着一个相当小的半径(比方说10厘米),这样就会浪费很多质量在橡胶上。然而,如果使用一个更大的气球,就像在布莱恩(Blaine)的升天特技表演一样,你会得到一个更好的氦橡胶比。
OK,准备工作基本完成了,现在我们来做一个粗略的估计。真实情况可能更加复杂,在此只是为了更直观的表达。首先,我们从橡胶密度1000公斤/立方米开始,这与水的密度基本相同(足够接近橡胶)。对于气球的半径,笔者将使用0.75米和0.2毫米的厚度。这就意味着,一个气球的净升力将是:
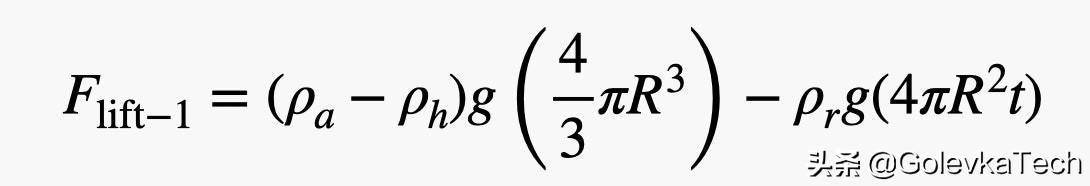
这可能从数值上听起来有点夸张,但事实并非如此。它等于排开的空气的重量减去氦气和橡胶的重量。现在,为了求出气球的数量,我们只需要把人的重量(这里使用了用大卫·布莱恩的体重,再加上质量为100公斤的随身设备)除以一个气球的提升力。下面这是使用python脚本运行的计算结果(如有兴趣,可自行在提供的VPython中改变数值)。

在线代码:
ht删tps://trin除ket.io/glow文script/0b8e字e46efb
和预想的一样,这个计算数值并不是很好。256个,对于一个在YouTube上直播引起世界级轰动的节目来说,这并不是一个史诗级的数字——与实际使用的52个气球相差甚远。当然,这显然说明计算中对气球厚度的估计,可能是完全偏离了——但是如果把半径改为1.5米会发生什么呢?结果得到了大约11个气球。这个数就看起来极为可观了。
简要说明:上面的计算提供了在线代码。如果有兴趣可自行使用,可以看到其中的估计值,并将其更改为任何你所预期的数值。然后点击开始按键,运行它。
问题三:气球会永远保持上升吗?很明显,没有什么事物是会永远持续下去的。一旦升力大于或等于整体向下拉的重力,气球的高度就会不断增加。并且,会发生变化的是升力,重力是基本可视为恒定不变的。在高空中,海拔越高则空气密度会越低。这就意味着,由于浮力等于被排开的空气重量,所以它会减小。

所以,气球最终会达到一个让它处于平衡状态的高度,它不会再往上升了。当然,这是假设气球的体积也保持不变的前提下得出的结论——但这在实际中是不正确的。在高海拔地区,大气压力会降低,对气球周围的推动力也会减小。这意味着气球内的氦气可以拉伸橡胶并使其膨胀,从而产生更大的浮力。也就是在某些时候,橡胶气球会拉伸至其极限,然后破裂。接下来所发生的就是我们熟知的情况,因为所有的氦气都会逸出,气球就只剩下一大块破碎的橡胶。最后从空中飘落下来。
问题四:起飞时的加速度是多少?首先,我们可以估计一下大卫·布莱恩(David Blaine)在开始上升时的垂直加速度。虽然直播的时候没有一个完美的摄像机角度,但我们可以大致估算出他在视频不同帧中的位置(以次粗略获得时间)。有了这个数据,我们就可以得到了下面的垂直位置与时间的函数图。

如果一个物体有一个恒定的加速度,那么它的位置可以用下面的运动学方程来计算。

这里重要的是,我们可以用这个方程来寻找垂直加速度的值。如果对数据拟合一个二次方程,t^2前面的系数必须等于这个运动方程中的(½)a项。这也就意味着,我们可以用拟合的方法来求加速度,所得到的数值大约是0.05m/s^2。在这里笔者跳过了一些步骤,如有兴趣的话可以自己试着推导一下。但是,这个数值是否真的有那么合理呢?
我们用另一种方法来处理这个问题,是否会得到近似的结果?接下来,我们来验证一下:首先,假设布莱恩(Blaine)处于平衡状态,F合力=0N。然后,他把一个1磅(4.4N)的小重量物体交给女儿。另外,别忘了算上他女儿多加的那个气球。但是,笔者觉得对于这个估算,我们可以只考虑递给他的重量。也就是说,他的重量减少了4.4N,得到的向上的净升力是4.4N。现在,我可以用牛顿第二定律来计算。
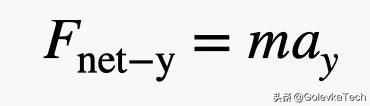
可以用牛顿第二定律来说明:
对于质量,需要布莱恩(Blaine)和气球的质量。假设这是110公斤。当力为4.4N时,垂直加速度为0.04m/s^2。对于该计算结果,这实际上比想象的要接近。可以验证该方法确实可行。
大卫·布莱恩(David Blaine)成功地让他的气球装置升到了超过7315.2米(24000英尺)的高度,并且他成功地通过跳伞回到了地面。从另一方面,这也解答我们儿时一直困惑已久的"气球飞天"梦想,在这里笔者用了初略分析计算验证了其的可行性,如有不足或疏忽之处,望各位多多指正!
撰写:GolevkaTech
重要声明:此处所发表的图文和视频均为作者的原创稿件,版权归原创作者所拥有。所刊发的图片和视频作品,除特别标注外,均视为图文作者和被拍摄者默认此版权之归属权。
,




