梯度下降法,是当今最流行的优化(optimization)算法,亦是至今最常用的优化神经网络的方法。与此同时,最新的深度学习程序库都包含了各种优化梯度下降的算法(可以参见如 lasagne、caffe 及 Kera 等程序库的说明文档)。但它们的算法则不被公开,都作为黑箱优化器被使用,这也就是为什么它们的优势和劣势往往难以被实际地解释。
本文旨在让你对不同的优化梯度下降法的算法有一个直观认识,以帮助你使用这些算法。我们首先会考察梯度下降法的各种变体,然后会简要地总结在训练(神经网络或是机器学习算法)的过程中可能遇到的挑战。接着,我们将会讨论一些最常见的优化算法,研究它们的解决这些挑战的动机及推导出更新规律(update rules)的过程。我们还会简要探讨一下,在平行计算或是分布式处理情况下优化梯度下降法的算法和架构。最后,我们会考虑一下其他有助于优化梯度下降法的策略。
在该方法中,每次更新我们都需要在整个数据集上求出所有的偏导数。因此批量梯度下降法的速度会比较慢,甚至对于较大的、内存无法容纳的数据集,该方法都无法被使用。同时,梯度下降法不能以「在线」的形式更新我们的模型,也就是不能再运行中加入新的样本进行运算。
批量梯度下降法的实现代码,如下所示:
for i in range(nb_epochs):
对于给定的迭代次数,我们首先基于输入的罚函数 loss_function 对输入的参数向量 params 计算梯度向量 params_grad。注意,最新的深度学习程序库中,提供了自动求导的功能,能够高效、快速地求给定函数对于特定参数的导数。如果你希望自己写代码求出梯度值,那么「梯度检查」会是一个不错的注意。(你可以参考这里,了解关于如何检查梯度的相关建议。)
然后,我们对参数减去梯度值乘学习率的值,也就是在反梯度方向,更新我们参数。当目标函数 J(θ) 是一凸函数时,则批量梯度下降法必然会在全局最小值处收敛;否则,目标函数则可能会局部极小值处收敛。
随机梯度下降法(Stochastic Gradient Descent)
相比批量梯度下降法,随机梯度下降法的每次更新,是对数据集中的一个样本(x,y)求出罚函数,然后对其求相应的偏导数:

因为批量梯度下降法在每次更新前,会对相似的样本求算梯度值,因而它在较大的数据集上的计算会有些冗余(redundant)。而随机梯度下降法通过每次更新仅对一个样本求梯度,去除了这种冗余的情况。因而,它的运行速度被大大加快,同时也能够「在线」学习。
随机梯度下降法更新值的方差很大,在频繁的更新之下,它的目标函数有着如下图所示的剧烈波动。
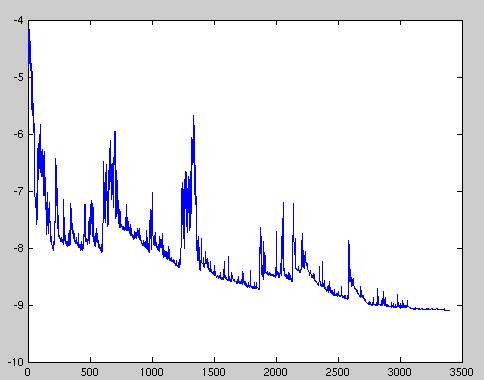
SGD 函数波动,来源:Wikipedia
相比批量梯度下降法的收敛会使目标函数落入一个局部极小值,SGD 收敛过程中的波动,会帮助目标函数跳入另一个可能的更小的极小值。另一方面,这最终会让收敛到特定最小值的过程复杂化,因为该方法可能持续的波动而不停止。但是,当我们慢慢降低学习率的时候,SGD 表现出了与批量梯度下降法相似的收敛过程,也就是说,对非凸函数和凸函数,必然会分别收敛到它们的极小值和最小值。
相比批量梯度下降法的代码,在如下的代码中,我们仅仅加入了一个循环,用以遍历所有的训练样本并求出相应的梯度值。注意,如这里所说,在每次迭代中,我们会打乱训练数据集。
for i in range(nb_epochs):
小批量梯度下降法(Mini-Batch Gradient Descent)
小批量梯度下降法集合了上述两种方法的优势,在每次更新中,对 n 个样本构成的一批数据,计算罚函数 J(θ),并对相应的参数求导:

这种方法,(a) 降低了更新参数的方差(variance),使得收敛过程更为稳定;(b) 能够利用最新的深度学习程序库中高度优化的矩阵运算器,能够高效地求出每小批数据的梯度。通常一小批数据含有的样本数量在 50 至 256 之间,但对于不同的用途也会有所变化。小批量梯度下降法,通常是我们训练神经网络的首选算法。同时,有时候我们也会使用随机梯度下降法,来称呼小批量梯度下降法(译者注:在下文中,我们就用 SGD 代替随机梯度下降法)。注意:在下文对于随机梯度法优化的介绍中,为方便起见,我们会省略式子中的参数 x(i:i n),y(i:i n)。
如下的代码所示,我们不再对每个样本进行循环,而是对每批带有 50 个样本的小批数据进行循环:
for i in range(nb_epochs):
面临的挑战
由于 Vanilla 小批量梯度下降法并不能保证良好地收敛,这给我们留下了如下待解决的挑战:
-
选择适当的学习率是一个难题。太小的学习率会导致较慢的收敛速度,而太大的学习率则会阻碍收敛,并会引起罚函数在最小值处震荡,甚至有可能导致结果发散;
-
我们可以设置一个关于学习率地列表,通过如退火的方法,在学习过程中调整学习率——按照一个预先定义的列表、或是当每次迭代中目标函数的变化小于一定阈值时来降低学习率。但这些列表或阈值,需要根据数据集地特性,被提前定义。
-
此外,我们对所有的参数都采用了相同的学习率。但如果我们的数据比较稀疏,同时特征有着不同的出现频率,那么我们不希望以相同的学习率来更新这些变量,我们希望对较少出现的特征有更大的学习率。
在对神经网络最优化非凸的罚函数时,另一个通常面临的挑战,是如何避免目标函数被困在无数的局部最小值中,以导致的未完全优化的情况。Dauphin 及其他人 [19] 认为,这个困难并不来自于局部最小值,而是来自于「鞍点」,也就是在一个方向上斜率是正的、在一个方向上斜率是负的点。这些鞍点通常由一些函数值相同的面环绕,它们在各个方向的梯度值都为 0,所以 SGD 很难从这些鞍点中脱开。
以下是其他几种经典的最优化方法,可用于神经网络等算法收敛到全局(或局部)最优解。
牛顿法
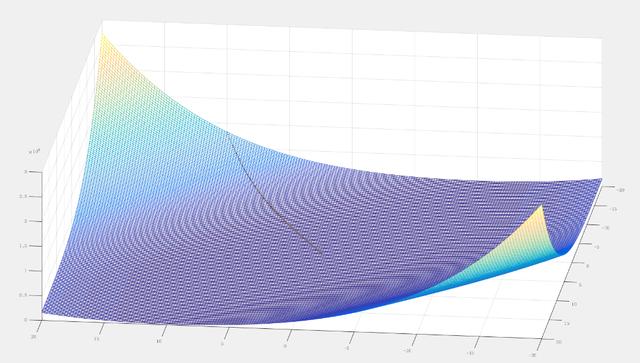
牛顿法是二阶算法,因为该算法使用了海塞矩阵(Hessian matrix)求权重的二阶偏导数。牛顿法的目标就是采用损失函数的二阶偏导数寻找更好的训练方向。现在我们将采用如下表示: f(wi) = fi、ᐁf(wi) = gi 和 Hf(wi) = Hi。在 w0 点使用泰勒级数展开式二次逼近函数 f。
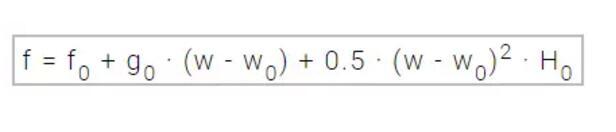
H0 为函数 f 在点 w0 的海塞矩阵。通过将 g 设定为 0,我们就可以找到 f(w) 的极小值,也就得到了以下方程式。
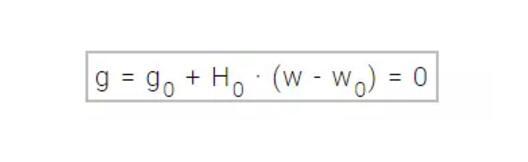
因此,从参数向量 w0 开始,牛顿法服从以下方式进行迭代:
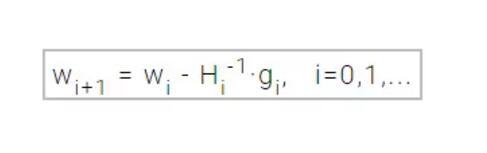
向量 Hi-1·gi(参考上式)也就是所说的牛顿下降步(Newton's step)。注意,参数的这些变化将朝着极大值而不是极小值逼近,出现这样的情况是因为海塞矩阵非正定。因此在不能保证矩阵正定的情况下,损失函数并不能保证在每一次迭代中都是减少的。为了防止上述问题,牛顿法的方程式通常可以修改为:
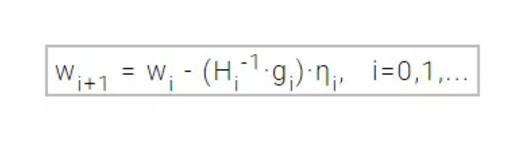
学习速率η同样可是设定为固定常数或通过单变量优化取值。向量 d=Hi-1·gi(参考上式)现在就称为牛顿训练方向(Newton's training direction)。
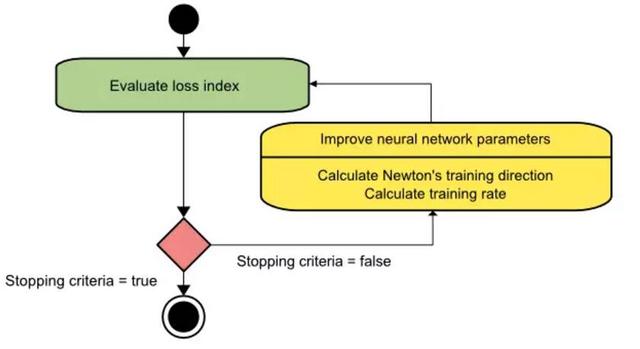
使用牛顿法的训练过程状态图就如下图所示。从此图可以看出来,系统首先通过获得牛顿训练方向,然后获得合适的学习速率来进行参数的更新优化。
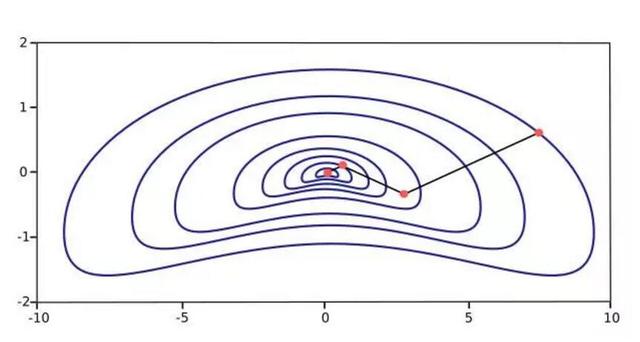
下面的梯度图展示了牛顿法的性能。因为牛顿法是采用其损失函数的二阶偏导数寻找更好的训练下降方向,所以它相比梯度下降只要更少的迭代次数就能下降到损失函数的极小值,因此函数收敛速度也会大幅度地加快。
然而,牛顿法的困难之处在于其计算量,因为对海塞矩阵及其逆的精确求值在计算量方面是十分巨大的。
共轭梯度法(Conjugate gradient)
共轭梯度法可认为是梯度下降法和牛顿法的中间物。该算法希望能加速梯度下降的收敛速度,同时避免使用海塞矩阵进行求值、储存和求逆获得必要的优化信息。
在共轭梯度训练算法中,因为是沿着共轭方向(conjugate directions)执行搜索的,所以通常该算法要比沿着梯度下降方向优化收敛得更迅速。共轭梯度法的训练方向是与海塞矩阵共轭的。
我们用 d 表示训练方向向量,然后从初始参数向量 w0 和初始训练方向向量 d0=-g0 开始,共轭梯度法所构建的训练方向序列为:
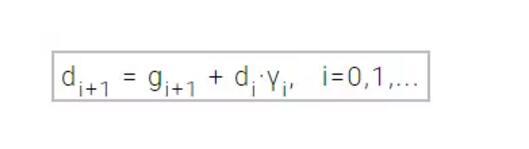
在上式中,γ 称之为共轭参数,并且有一些方法计算这个参数。两种最常用的方法是源自 Fletcher、Reeves 和 Polak 、Ribiere。对于所有的共轭梯度算法,训练方向周期性地重置为负梯度向。
参数通过下面的表达式得以更新和优化。通常学习速率η可使用单变量函数优化方法求得。
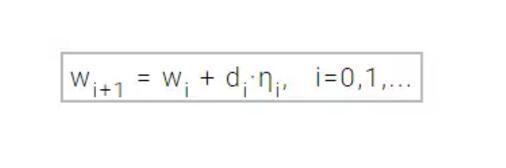
共轭梯度法的训练过程流程图就如下所示。从图中我们可以看出来模型是通过第一次计算共轭梯度训练方向而优化参数的,然后再寻找适当的学习速率。
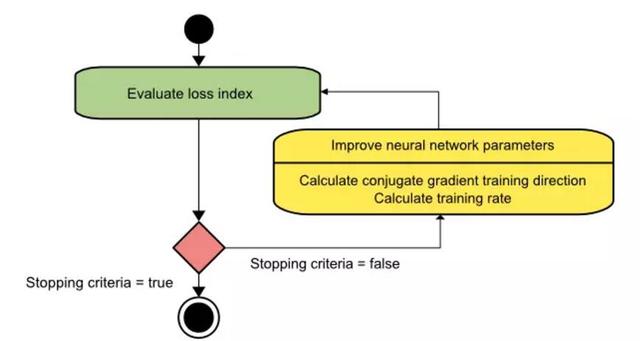
共轭梯度法已经证实其在神经网络中要比梯度下降法有效得多。并且由于共轭梯度法并没有要求使用海塞矩阵,所以在大规模神经网络中其还是可以做到很好的性能。
拟牛顿法(Quasi-Newton method)
因为需要很多的操作求解海塞矩阵的值还有计算矩阵的逆,应用牛顿法所产生的计算量是十分巨大的。因此有一种称之为拟牛顿法(quasi-Newton)或变量矩阵法来解决这样的缺点。这些方法并不是直接计算海塞矩阵然后求其矩阵的逆,拟牛顿法是在每次迭代的时候计算一个矩阵,其逼近海塞矩阵的逆。最重要的是,该逼近值只是使用损失函数的一阶偏导来计算。
海塞矩阵由损失函数的二阶偏导组成,拟牛顿法背后的思想主要是仅使用损失函数的一阶偏导数,通过另一矩阵 G 逼近海塞矩阵的逆。拟牛顿法的公式可以表示为:
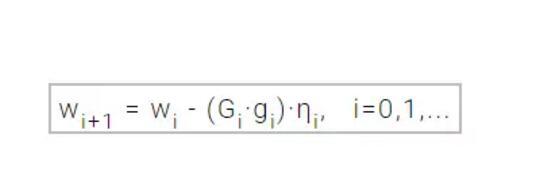
学习速率 η可以设定为固定常数,也可以通过单变量函数优化得到。其中矩阵 G 逼近海塞矩阵的逆,且有不同的方式进行逼近。通常,最常用的两种方式是 Davidon–Fletcher–Powell formula (DFP) 和 the Broyden–Fletcher–Goldfarb–Shanno formula (BFGS)。
拟牛顿法的训练过程流程图就如下所示。从图中我们可以看出来模型是通过第一次计算拟牛顿训练方向而优化参数的,然后再寻找适当的学习速率。
拟牛顿法适用于绝大多数案例中:它比梯度下降和共轭梯度法收敛更快,并且也不需要确切地计算海塞矩阵及其逆矩阵。
Levenberg-Marquardt 算法
Levenberg-Marquardt 算法,也称之为衰减最小二乘法(damped least-squares method),该算法的损失函数采用平方误差和的形式。该算法的执行也不需要计算具体的海塞矩阵,它仅仅只是使用梯度向量和雅可比矩阵(Jacobian matrix)。
该算法的损失函数如下方程式所示为平方误差和的形式:

在上式中,m 是数据集样本的数量。
我们可以定义损失函数的雅可比矩阵以误差对参数的偏导数为元素,如下方程式所示:
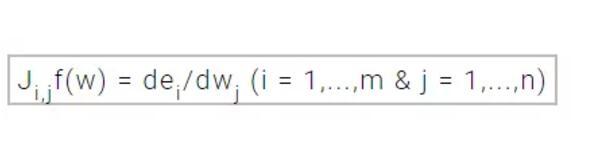
其中 m 是数据集样本的数量,n 是神经网络的参数数量。那么雅可比矩阵就是 m×n 阶矩阵。
损失函数的梯度向量就可以按如下计算出来:
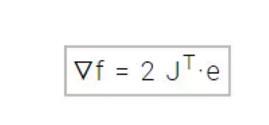
e 在这里是所有误差项的向量。
最终,我们可以用以下表达式逼近海塞矩阵:

其中λ为衰减因子,它确保了海塞矩阵的正定性(positiveness),I 是单位矩阵。
下面的表达式定义了 Levenberg-Marquardt 算法中参数的更新和优化过程:
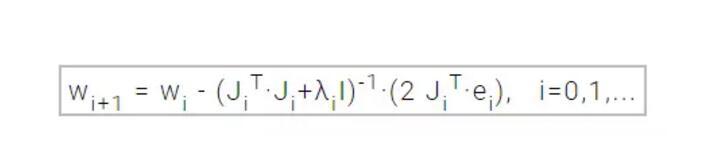
当衰减参数λ为 0 时,Levenberg-Marquardt 算法就是使用海塞矩阵逼近值的牛顿法。而当 λ很大时,该算法就近似于采用很小学习速率的梯度下降法。如果进行迭代导致了损失函数上升,衰减因子λ就会增加。如果损失函数下降,那么λ就会下降,从而 Levenberg-Marquardt 算法更接近于牛顿法。该过程经常用于加速收敛到极小值点。
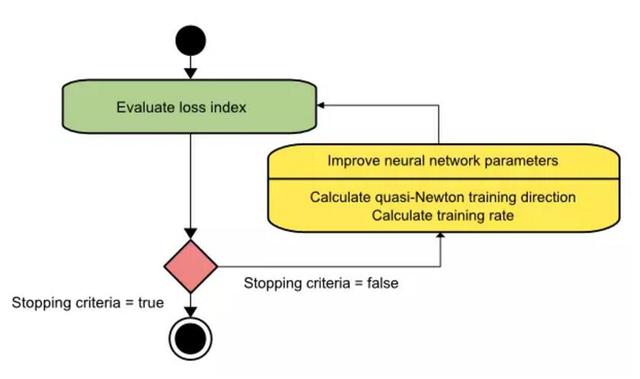
使用 Levenberg-Marquardt 法的神经网络训练过程状态图就如下图所示。第一步就是计算损失函数、梯度和海塞矩阵逼近值,随后再在每次迭代降低损失中调整衰减参数。
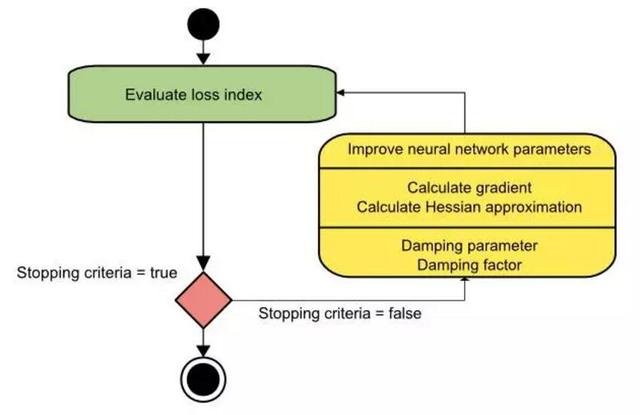
正如我们所了解到的,Levenberg-Marquardt 算法是为平方误差和函数所定制的。这就让使用这种误差度量的神经网络训练地十分迅速。然而 Levenberg-Marquardt 算法还有一些缺点,第一就是其不能用于平方根误差或交叉熵误差(cross entropy error)等函数,此外该算法还和正则项不兼容。最后,对于大型数据集或神经网络,雅可比矩阵会变得十分巨大,因此也需要大量的内存。所以我们在大型数据集或神经网络中并不推荐采用 Levenberg-Marquardt 算法。
,




