我们之前对极限的所有知识点
都做了详细的介绍
我们今天就从题型与解法出发
为同学们介绍下
极限中四种常见的题型与解法
ps:拿出你们的小本本,我们要发车了!

等价无穷小
基本公式:

注:
看到指数类型的极限题目,并且括号里面趋近于“1”时,首选取e的重要极限方法。
解题的核心是指数的配凑,配凑成与括号中对应的形式。
例题1

等价无穷小
基本公式:

注意:
-
所有的等价无穷小都是在x→0时才可以使用的;
-
加减法不可以使用等价无穷小,要使用泰勒公式。
例题2


泰勒公式
基本公式:


例题3

例题4

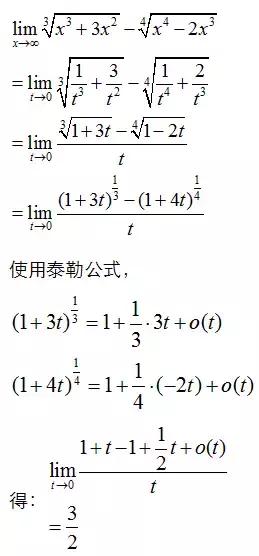

洛必达法则
注:
-
洛必达法则的使用条件是分子分母都趋向于“0”或者“∞”时,才可以使用;
-
一个式子能等价无穷小的先等价无穷小,再使用洛必达法则会方便很多。
例题5

内容介绍到这里
一起来看昨日习题
上期习题

答案解析






