中点是几何中的一个重要概念,体现了对称、和谐之美,是中考的核心考察对象之一,在命题中占着重要的一席之地. 很多同学遇到几何题就头疼,很大的原因是没有掌握一些解题模型,也就是套路。在此特殊防控新型肺炎疫情的寒假阶段,通过系统学习归纳好总结文章的学习,再辅助必要练习,在家自主学习也是突破几何中难点行之有效的策略,也能学得精彩。
本文拟从与三角形中点有关的基本定理、基本图形等入手,以最新考题为例,对中点问题展开解法探究.

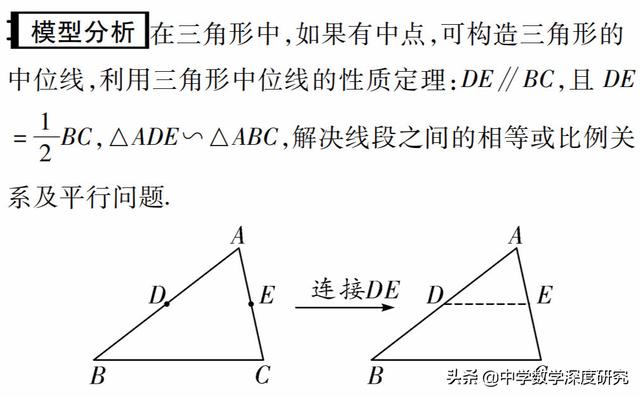
模型一 多个中点出现或平行 +中点(中点在平行线上)时,常考虑或构造三角形中位线
1.(2020•郑州模拟)如图,在△ABC中,BC=6,E,F分别是AB,AC的中点,动点P在射线EF上,BP交CE于点D,∠CBP的平分线交CE于点Q,当CQ=1/3CE时,EP BP的值为( )
A.6 B.9 C.12 D.18

【解析】延长BQ交射线EF于M,根据三角形的中位线平行于第三边可得EF∥BC,根据两直线平行,内错角相等可得∠M=∠CBM,再根据角平分线的定义可得∠PBM=∠CBM,从而得到∠M=∠PBM,根据等角对等边可得BP=PM,求出EP BP=EM,再根据CQ=1/3CE求出EQ=2CQ,然后根据△MEQ和△BCQ相似,利用相似三角形对应边成比例列式求解即可.故选:C.
2.(2019春•睢宁县期中)如图,在△ABC中,AE平分∠BAC,BE⊥AE于点E,点F是BC的中点.

(1)如图1,BE的延长线与AC边相交于点D,求证:EF=1/2(AC﹣AB);
(2)如图2,请直接写出线段AB、AC、EF的数量关系.
【解析】(1)先证明AB=AD,根据等腰三角形的三线合一,推出BE=ED,根据三角形的中位线定理即可解决问题.
(2)结论:EF=1/2(AB﹣AC),先证明AB=AP,根据等腰三角形的三线合一,推出BE=ED,根据三角形的中位线定理即可解决问题.
理由:如图2中,延长AC交BE的延长线于P.

∵AE⊥BP,∴∠AEP=∠AEB=90°,
∴∠BAE ∠ABE=90°,∠PAE ∠APE=90°,
∵∠BAE=∠PAE,∴∠ABE=∠ADE,∴AB=AP,
∵AE⊥BD,∴BE=PE,
∵BF=FC,
∴EF=1/2PC=1/2(AP﹣AC)=1/2(AB﹣AC).
模型二 直角三角形中遇到斜边上的中点,常联想“斜边上的中线等于斜边的一半”

3.(2019秋•高港区校级月考)如图,Rt△ABC中,∠CAB=90°,D是AB上一点(不与A.B重合),DE⊥BC于E,若P是CD的中点.
(1)请判断△PAE的形状,并说明理由;
(2)若△PAE为等边三角形,求∠ACB的度数.

【解析】(1)△PAE的形状为等腰三角形.
由Rt△DAC斜边上的中线性质得出PA=PC=1/2CD,由Rt△DEC斜边上的中线性质得出PE=PC=1/2CD,所以PA=PE,即得出结论;
(2)∵PC=PA=PE,∴∠ACP=∠CAP,∠PCB=∠PEC,
∴∠ACB=∠ACP ∠BCP=1/2×(180°﹣60°﹣60°)=30°.
4.(2019•福建模拟)已知点P是Rt△ABC斜边AB所在直线上的一个不与A、B重合的动点,分别过A、B向直线CP作垂线,垂足分别为E、F,点Q为斜边AB的中点
(1)当点P与点Q重合时,AE与BF的位置关系是______,QE与QF的数量关系是_____,并说明理由;
(2)当点P不与点Q重合时,判断QE与QF的数量关系并给予证明.
【解析】(1)如图1,当点P与点Q重合时,AE与BF的位置关系是AE∥BF,QE与QF的数量关系是AE=BF,
根据AAS推出△AEQ≌△BFQ,推出AE=BF即可;
(2)①当点P在线段AB上不与点Q重合时,QE=QF,
②当点P在线段BA(或AB)的延长线上时,此时(2)中的结论成立,
延长EQ交BF于D,求出△AEQ≌△BDQ,根据全等三角形的性质得出EQ=QD,根据直角三角形斜边上中点性质得出即可;延长EQ交FB于D,求出△AEQ≌△BDQ,根据全等三角形的性质得出EQ=QD,根据直角三角形斜边上中点性质得出即可.


模型三 等腰三角形中遇到底边上的中点,常联想“三线合一”的性质

5.(2019秋•海淀区校级期中)已知:在△ABC中,∠B=∠C,D,E分别是线段BC,AC上的一点,且AD=AE,
(1)如图1,若∠BAC=90°,D是BC中点,则∠2的度数为______;
(2)借助图2探究并直接写出∠1和∠2的数量关系______.

【解析】(1)根据三角形的一个外角等于和它不相邻的两个内角的和,∠AED=∠EDC ∠C,∠ADC=∠B ∠BAD,再根据等边对等角的性质∠B=∠C,∠ADE=∠AED,进而得出∠BAD=2∠CDE. ∠2的度数为22.5° ;
(2)根据三角形的一个外角等于和它不相邻的两个内角的和,∠AED=∠EDC ∠C,∠ADC=∠B ∠BAD,再根据等边对等角的性质∠B=∠C,∠ADE=∠AED,进而得出∠BAD=2∠CDE.∠1=2∠2
6.(2019秋•南昌期中)在△ABC中,AB=AC,点D在边BC上,点E在边AC上,且AD=AE.
(1)如图1,当AD是边BC上的高,且∠BAD=30°时,求∠EDC的度数;
(2)如图2,当AD不是边BC上的高时,请判断∠BAD与∠EDC之间的关系,并加以证明.

【解析】(1)由AD是边BC上的高,得到∠ADC=90°,根据等腰三角形的性质得到即可得到结论,∠EDC=15°;
(2)∠BAD=2∠EDC.
根据等腰三角形的性质得到∠B=∠C,∠ADE=∠AED,根据三角形外角的性质得到∠ADC=∠B ∠BAD,∠AED=∠C ∠EDC,于是得到结论.

模型四 遇到三角形一边垂线过这边中点时,可以考虑用垂直平分线的性质

7.(2019秋•沛县期中)如图,在△ABC中,∠C=90°,点P在AC上运动,点D在AB上,PD始终保持与PA相等,BD的垂直平分线交BC于点E,交BD于点F,连接DE.
(1)判断DE与DP的位置关系,并说明理由;
(2)若AC=6,BC=8,PA=2,求线段DE的长.

【解析】(1)DE⊥DP。
连接OD,根据等腰三角形的性质得到∠A=∠PDA,根据线段垂直平分线的性质得到EB=ED,于是得到结论;
(2)连接PE,设DE=x,则EB=ED=x,CE=8﹣x,根据勾股定理即可得到结论.则DE=4.75.
8.(2019春•张店区期末)如图,AB垂直平分线段CD(AB>CD),点E是线段CD延长线上的一点,且BE=AB,连接AC,过点D作DG⊥AC于点G,交AE的延长线与点F.
(1)若∠CAB=α,则∠AFG=______(用α的代数式表示);
(2)线段AC与线段DF相等吗?为什么?
(3)若CD=6,求EF的长.

【解析】(1)根据等腰三角形的性质得到∠BAE=∠AEB=45°,根据三角形的内角和即可得到结论;
(2)连接AD,根据线段垂直平分线的性质得到AC=AD,求得∠ADC=∠ACB=α,于是得到AC=DF;
(3)根据已知条件得到BD=CB=3,过F作FH⊥CE交CE的延长线于H,得到△EHF是等腰直角三角形,求得FH=HE,根据全等三角形的性质即可得到结论.EF=3√2.

模型五 遇到三角形一边上的中点(中线或与中点有关的线段),考虑倍长中线法构造全等三角形

9.(2019秋•南京月考)小明遇到这样一个问题,如图1,△ABC中,AB=7,AC=5,点D为BC的中点,求AD的取值范围.

小明发现老师讲过的"倍长中线法"可以解决这个问题,所谓倍长中线法,就是将三角形的中线延长一倍,以便构造出全等三角形,从而运用全等三角形的有关知识来解决问题的方法,他的做法是:如图2,延长AD到E,使DE=AD,连接BE,构造△BED≌△CAD,经过推理和计算使问题得到解决.
请回答:(1)小明证明△BED≌△CAD用到的判定定理是:______(用字母表示)
(2)AD的取值范围是________.
小明还发现:倍长中线法最重要的一点就是延长中线一倍,完成全等三角形模型的构造.
参考小明思考问题的方法,解决问题:
如图3,在正方形ABCD中,E为AB边的中点,G、F分别为AD,BC边上的点,若AG=2,BF=4,∠GEF=90°,求GF的长.
【解析】(1)根据SAS即可证明△BED≌△CAD.
(2)在△ABE利用三边关系定理即可解决.
解决问题:延长GE交CB的延长线于M.只要证明△AEG≌△BEM,推出AG=CM=2,再根据线段的垂直平分线的性质,即可解决问题.

∵四边形ABCD是正方形,∴AD∥CM,∴∠AGE=∠M,
易证△AEG≌△BEM(AAS),∴GE=EM,AG=BM=2,
∵EF⊥MG,∴FG=FM,
∵BF=4,∴MF=BF BM=2 4=6,∴GF=FM=6.

模型六 中线等分三角形面积

10.我们知道三角形一边上的中线将这个三角形分成两个面积相等的三角形.如图1,AD是△ABC边BC上的中线,则S△ABD=S△ACD.

(1)如图2,△ABC的中线AD、BE相交于点F,△ABF与四边形CEFD的面积有怎样的数量关系?为什么?
(2)如图3,在△ABC中,已知点D、E、F分别是线段BC、AD、CE的中点,且S△ABC=8,求△BEF的面积S△BEF



方法综述
中点常常可以与等腰三角形、直角三角形等结合,还可以与另一个中点构成中位线模型,或者采取倍长中线等方法,这些都是处理中点问题的常见策略.在解决与中点有关的问题中,大家可以联想这些基本图形,构造相应辅助线,勇于尝试,敢于探索.
,




