本期继续连载数学基础的最后一部分:概率论,包括基础概念、似然、最大似然估计、概率分布衡量等。至此数学基础知识就介绍完啦,下次开始介绍具体的模型算法。
《机器学习基础知识手册》总结了更多的问题,欢迎访问github地址:https://github.com/5663015/machine-learning-handbook
概率论基础概念- 排列:,组合:
- 联合概率分布:多个变量的概率分布称为联合概率分布,表示和同时发生的概率。
- 边缘概率:有时我们知道了一组变量的联合概率分布,还需要知道其中一个子集的概率分布,这种定义在子集上的概率分布称为边缘概率分布。对于离散型随机变量,根据下面的求和法来计算:
- 条件概率:在给定和发生的条件概率为:
- 全概率公式:若事件构成一个完备事件组且都有正概率,则对于任一个事件x都有如下全概率公式:
- 贝叶斯公式:贝叶斯公式是关于随机事件x和y的条件概率和边缘概率边缘概率的:
是后验概率,是条件概率或似然
- 期望:对于N个离散随机变量X,其概率分布为,X的期望定义为:
对于连续型随机变量X,概率密度函数为,则期望为:
期望的性质:
- 方差:随机变量X的方差用来定义它的概率分布的离散程度,定义为:
方差的性质:
概率和似然的区别与联系- 概率表达的是给定下样本随机向量的可能性,而似然表达了给定样本下参数为真实值的可能性。
- 似然函数的形式是,其中"|"代表的是条件概率或者条件分布,因此似然函数是在"已知"样本随机变量的情况下,估计参数空间中的参数的值,因此似然函数是关于参数的函数,即给定样本随机变量后,估计能够使的取值成为的参数的可能性;而概率密度函数的定义形式是,即概率密度函数是在“已知”的情况下,去估计样本随机变量出现的可能性。
- 似然函数可以看做是同一个函数形式下的不同视角。以函数为例,该函数包含了两个变量,和,如果已知为2,那么函数就是变量的二次函数,即 ;如果已知为2,那么该函数就是变量b的幂函数,即。同理,和也是两个不同的变量,如果的分布是由已知的刻画的,要求估计的实际取值,那么就是的概率密度函数;如果已知随机变量的取值,而要估计使取到已知的参数分布,就是似然函数的目的。
- 对于函数有两种情况:
- 保持不变,为变量,此时函数为概率函数,表示的是出现的概率;
- 是变量,是变量,此时为似然函数,表示不同下出现的概率
- 最大似然估计尝试求解使得出现概率最高的。对于m次实验,由于每次都是独立的,我们可以将中每一次实验结果的似然函数全部乘起来,那么,使得该式取得最大值的,即为的最大似然估计:
- 最大似然估计方法尝试求解来最大化似然函数,显然计算出来的参数完全取决于实验结果。最大后验概率能够很大程度解决这个问题。该方法尝试最大化后验概率:
是已知的,只需最大化分子部分。和最大化似然的唯一区别是增加了先验概率
KL散度、JS散度、Wasserstein距离- KL散度(不对称),也叫相对熵,衡量分布之间的差异性。KL散度并不是一个真正的距离,KL散度不满足对称性(即)和三角不等式(即不满足)
将KL散度展开可得,其中为熵,为交叉熵。KL散度实际上衡量的是两者之间的信息损失
- KL散度的缺点:
- 无界
- 不对称
- 若两个分布无重叠部分可能得到的结果无意义
关于分布不重合时的情况举例,对于如下的分布,P1在AB上均匀分布,P2在CD上均匀分布,控制着两个分布的距离远近。可得:
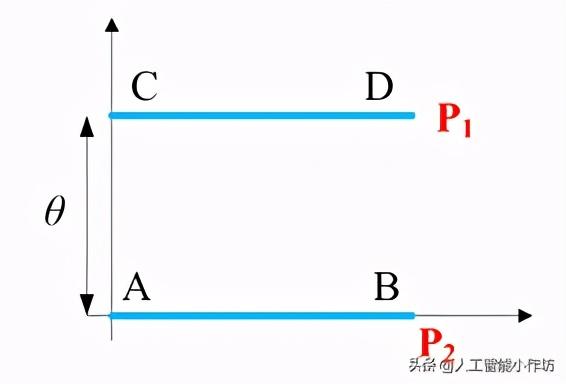
- JS散度:解决了KL散度非对称的问题。KL散度和JS散度都有一个问题,即当两个分布和离得很远没有重叠时,KL散度是无意义的,JS散度是个常数。
- Wasserstein距离:
是分布组合起来的所有可能的联合分布的集合。对于每一个可能的联合分布,可以从中采样得到一个样本x和y,并计算出这对样本的聚类,所以可以计算该联合分布下,样本对距离的期望值。在所有可能的联合分布中能够取到这个期望值的下界的就是wasserstein距离。直观上可以理解为在这个路径规划下把土堆挪到土堆所需要的消耗。而Wasserstein距离就是在最优路径规划下的最小消耗,也叫做Earth-mover距离。
机器学习面试题精选连载(1)——模型基础
机器学习面试题精选连载(2)——微积分与线性代数
机器学习面试题精选连载(3)——线性代数
,




