
作者 | 林开亮
在数论中,有许多有趣的难题,有些已经解决了,如著名的费马大定理,它断言,当 时,不存在满足 的正整数 。英国数学家怀尔斯对这个问题的解决,是 20 世纪数学的一项重要成就。
不过,还有一些说起来简单、做起来困难的数论问题仍未解决,比如我们这里要介绍的三立方数之和的问题。
1957 年,英国数学家莫德尔(Mordell)问:哪些正整数可写成三个立方数(这个立方数可正可负也可以等于 0)之和?
容易看出,前三个正整数都可以写成三个立方数之和:
而且,3 还有另一种写法:
至于接下来两个数 4,5, 利用一个简单的推理,可以说明它们都不能表示成三个立方数的和。事实上,可以证明,所有形如 (其中 是整数)的数都不能写成三个立方数之和。原因在于,任何一个立方数除以 9 的余数只能是 或 。推理如下:若 ,则 ,它被 9 整除;若 ,则
它被 9 除余 1;若 ,则
它被 9 除余 。于是,三个立方数之和除以 9 的余数只能由取自 中的三个数求和得到,从而不可能得 或 。
接下来考虑 ,不难发现
到 12 就不太容易了,事实上它也可以(你可以试一试软件,如 https://www.wolframalpha.com/):
至于接下来的两个数,13 和 14,注意 肯定不能写成三个立方数之和。到 15,16, 17,18,19,20 又变得容易了:
到 21 又要求助软件了:
22 与 23 被 9 除余数分别为 4 和 5,不必考虑,接下来我们有
接下来到 30 了,求助一般的软件可能也帮不上忙了。事实上,直到 1999 年,哈佛大学的数论专家 Noam D. Elkies 以及佐治亚大学的四个研究生组成的团队才各自独立地给出 30 分解为 3 个立方数之和的表达式(都是基于 Elkies1996 年提出的算法):
一般而言,对给定的正整数 ,假定它除以 9 的余数不是 ,要将它分解为 3 个立方数之和这个问题是很困难的。例如,像
也是到了 1992 年,才由 Heath-Brown, Lioen, te Riele 基于 Heath-Brown 的深刻算法给出.
到 2008 年,数学家已经对 1000 以下的满足除以 9 余数不是 的正整数 , 求出了将 分解为 3 个立方数之和的表达式,除了以下 14 个数未知:
2016 年,Sander G. Huisman 第一个得到 的分解
2019 年,Andrew Booker 第一个得到 的分解:

2019 年 9 月,Booker 与 MIT 的数学家 Andrew Sutherland 合作,首次得到 与 的分解:
此外,他们还得到了 3 的一个意想不到的分解:
这就对 Mordell 1953 年提出的一个问题给出了回答. Mordell 曾经问, 除了已知的两组整数解 之外,是否还有其它解?Booker 和 Sutherland 的上述结果对此给出了肯定回答.
目前所有的结果与努力似乎都在支持 Heath-Brown 1992 年提出的下述猜想:
Heath-Brown 猜想: 设 是一个正整数,且除以 9 的余数不等于 或 ,那么存在无穷多个三元整数组 满足方程
在 (其中 为正整数)的特殊情况,这个猜想是成立的。这是因为,数学家 A. S. Werebrusov(1908 年)与 K. Mahler(1936 年)分别给出了以下两个参数解(分别对应于 与 ):
Heath-Brown 猜想有一个弱的版本,即:当正整数 满足同样的同余条件时, 有整数解。可即便是对于这个弱版本的猜想,我们目前也没有很好的方法对付。例如,对 1000 以内的数,我们还有 10 个尚不能确定是否如此,这 10 个数是
位于榜首的是 114. 考虑到有朋友可能忍不住要动手试一试,我建议大家还是先不要轻举妄动,因为数学家已经用计算机运行高效的算法搜索了绝对值在 以内的整数了!对于较小的 ,此处有一些结果: http://www.asahi-net.or.jp/~KC2H-MSM/mathland/math04/cube01.htm。跟费马大定理一样,这问题初看起来是业余爱好者都可以做的,可实际上远非如此.
例如,我们前面提到的哈佛大学的数论专家 Noam D. Elkies, 他 1987 年(20 岁)博士毕业于哈佛,1993 年(26 岁)成为哈佛正教授,是哈佛历史上最年轻的正教授。而他最成名的一项工作,是在 1988 年(当时在哈佛做博士后)利用椭圆曲线发现的一个结果:
从而否定了大数学家欧拉在 1769 年(距今恰好 250 年)提出的一个猜想。差不多同一时期,德国数学家 Don Zagier 也独立得到同样的结果.
与上述问题相关,我还想介绍一下其他三个问题.
问题 1:是否每个正整数都可以写成 4 个立方数(可正可负也可取零)之和?
这是关于立方数的带正负号的华林问题,已知的结果是,每个正整数都可以写成 5 个立方数之和。其推导也很简单,我们从华罗庚《数论导引》引述如下。注意,对正整数 , 总可以被 6 整除,于是设 。注意到有恒等式
从而 可以写成
问题 1 相当于问,5 是不是最优的?人们倾向于猜测 5 不是最优,4 个就足以.
问题 2:是否每个充分大的正整数都可以写成 4 个正立方数之和?
(事实上,Dickson 在 1939 年曾证明,这两个数是仅有的例外。这是立方数华林问题的渐进版本。关于立方数的华林问题的结果是:每个正整数都可以写成 9 个正立方数的和。其中 9 是最优的,即存在正整数不能写成 8 个立方数的和,例如 23 与 239。)德国数学家 Landau 在 1909 年证明了,所有充分大的正整数都可以写成 8 个立方数之和。1943 年,苏联数学家 Linnik 证明了,所有充分大的正整数都可以写成 7 个立方数之和。事实上,2016 年,S. Siksek 证明了,每个大于 454 的正整数都可以写成 7 个立方数之和(Every integer greater than 454 is the sum of at most seven positive cubes, Algebra & Number Theory 10 ,2016)。
人们猜测:每个充分大的正整数都可以写成 4 个正立方数之和。甚至有人猜测,只要 , 就可以写成 4 个正立方数之和.
跟华林问题一样,问题 1 与问题 2 都可以推广到四次方数、五次方数等等,有兴趣的读者可参见华罗庚《数论导引》第 18 章。
下面的问题,可以视为弱化的 Heath-Brown 猜想的一个变种。
问题 3:是否每个正整数都可以写成 3 个形如
的数之和?
华罗庚在 1935 年曾证明,每个正整数都可以无穷多种方式写成 7 个形如 的数之和。这个结果可以改进为:每个正整数都可以写成 4 个形如 的数之和;每个正整数都可以无穷多种方式写成 6 个形如 的数之和。证明如下:事实上,对任意的整数 , 有
以及
容易看到,存在正整数不能写成 的形式,例如 。于是要表出所有的正整数,至少需要 3 个形如 的求和项。我们斗胆猜测,3 个就够了(即,问题 3 的回答是肯定的)。利用软件,不难测试出,这对许多正整数都是对的。(对于比较小的 ,有兴趣的读者可自行在 WolframAlpha 上测试.)例如,我们有

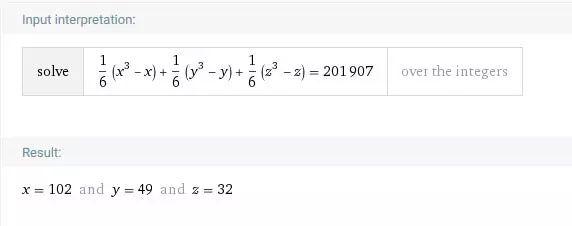


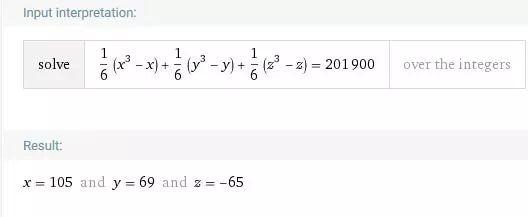






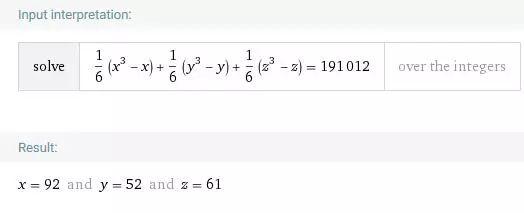
转载自“好玩的数学”微信公众平台

数学英才
中学生英才计划
数学学科官方公众号
推送数学微慕课和学习资料
shuxueyingcai
,




