什么是蝴蝶定理?我们先来看一下动图。

蝴蝶定理动态效果
上图是不是像一只蝴蝶扇动两只翅膀。
蝴蝶定理(Butterfly Theorem),是古代欧氏平面几何中最精彩的结果之一。这个命题最早出现在1815年,由W.G.霍纳提出证明。而“蝴蝶定理”这个名称最早出现在《美国数学月刊》1944年2月号,题目的图形像一只蝴蝶。这个定理的证法不胜枚举,至今仍然被数学爱好者研究,在考试中时有各种变形。
下面我们从以下几个方面来了解蝴蝶定理:
1、蝴蝶定理定义;
2、蝴蝶定理及其证明;
3、蝴蝶定理变形;
4、蝴蝶定理运用。
首先,我们来看蝴蝶定理是怎么定义的。
1、蝴蝶定理:AB是圆的一条弦,中点记为S,圆心为O,过S作任意两条弦CD、EF,分别交圆于C、D、E、F,连接CF、ED分别交AB于点M、N,求证:MS=NS。

蝴蝶定理:不管C、E点怎么在圆O上运动,始终有MS=NS。
2、蝴蝶定理及其证明
定理:如图,过圆中弦AB的中点M任引两弦CD和EF,连接CF和ED,分别交AB于P、Q,则PM=MQ。

蝴蝶定理证明途径:点Q与Q'重合
证明:过点M作直线AB的垂线I,作直线CF关于直线I的对称直线交圆于点C’、F’,交线段AB于点Q’。连接FF’、DF’、Q’F’、DQ’。据圆的性质和图形的对称性可知:
∠MF’Q’=∠MFP,∠F’Q’M=∠FPM;
且FF’//AB,PM=MQ’。
∵C、D、F’、F四点共圆,
∴∠CDF’ ∠CFF’=180°,
而由FF’//AB可得∠Q’PF ∠CFF’=180°,
∴∠CDF’=∠Q’PF,即∠MDF’=∠Q’PF,
又∵∠Q’PF=∠PQ’F’,即∠Q’PF=∠MQ’F’,
∴∠MDF’=∠MQ’F’。
这说明Q’、D、F’、M四点共圆,既得∠MF’Q’=∠Q’DM。
∵∠MF’Q’=∠MFP,
∴∠MFP=∠Q’DM。
而∠MFP=∠EDM,
∴∠EDM=∠Q’DM。
这说明点Q与点Q’重合,既得PM=MQ。
此定理还可用解析法来证明:
想法:设法证明直线DE和CF在x轴上的截距互为相反数。
证:以AB所在直线为x轴,线段AB的垂直平分线为y轴建立直角坐标系,M点是坐标原点。
设直线DE、CF的方程分别为
x=m1y n1,x=m2y n2;
直线CD、EF的方程分别为
y=k1x,y=k2x。
则经过C、D、E、F四点的曲线系方程为
(y=k1x)(y-k2x) λ(x-m1y n1)(x-m2y n2)=0。
整理得
(λ k1k2)x2 (1 λm1m2)y2-[(k1 k2) λ(m1 m2)]xy-λ(n1 n2)x λ(n1m2 n2m1)y λn1n2=0。
由于C、D、E、F四点在一个圆上,说明上面方程表示的是一个圆,所以必须
λ k1k2=1 λm1m2≠0,
且(k1 k2) λ(m1 m2)=0。
若λ=0,则k1k2=1,k1 k2=0,这是不可能的,故λ≠0;
又y轴是弦AB的垂直平分线,则圆心应落在y轴上,故有λ(n1 n2)=0,从而得n1 n2=0。
这说明直线DE、CF在x轴上的截距互为相反数,既得PM=MQ。
注:利用曲线系方程解题是坐标法的一大特点,它可以较好地解决直线与曲线混杂在一起的问题。如本题,四条直线方程一经组合就魔术般地变成了圆方程,问题瞬息间得以解决,真是奇妙,运用它解题,不拘泥于小处,能够从整体上去考虑问题。
另外,待定系数法在其中扮演了非常重要的角色,需注意掌握其用法。
当然上述只列举了蝴蝶定理的两种证明,证明方法还有很多,如:霍纳证法、作图法、对称法、面积法、帕斯卡证法、相似法、射影法等不再一一列举,大家可以自己试试其它证明方法。
3、蝴蝶定理变形
(1)过圆中弦AB的中点M引任意两弦CD和EF,连接CE和DF分别交AB的延长线于Q、P,则PM=QM。

过圆中弦AB的中点M引任意两弦CD和EF,连接CE和DF分别交AB的延长线于Q、P,则PM=QM。
简证:作DJ//AB,
由平行弦的性质得:JM=DM;
∠AMD=∠JMQ;
又∠AMD ∠JDM=180°;
∠JDM=∠CEJ,∠CEJ ∠JEQ=180°;
推出∠JMQ=∠JEQ,
∴J、Q、E、M四点共圆;
推出∠CEF=MJQ=∠MDP
推出△PDM≌△QJM;
∴PM=QM。
(2)(圆外蝴蝶定理)AB为⊙O外一直线,OM⊥AB于M,过M任作两条割线CD、EF,CF与ED分别与AB交于P、Q,则PM=QM。

(圆外蝴蝶定理)AB为⊙O外一直线,OM⊥AB于M,过M任作两条割线CD、EF,CF与ED分别与AB交于P、Q,则PM=QM。
简证:作JE//AB,导角得:J、C、B、P四点共圆;
推出∠MJP=∠DCP=∠DFE;
推出△JMP≌△EMQ;
推出PM=QM。
(3)(退化形式)如图,PA是△ABC外接⊙O的切线,过点P作OP的垂线与直线AB,AC分别交于E,F。求证:PE=PF。

(退化形式)如图,PA是△ABC外接⊙O的切线,过点P作OP的垂线与直线AB,AC分别交于E,F。求证:PE=PF。
简证:作JB//EF;
由垂径定理可证:BP=JP;
∠BPF=∠JBP=∠BJP=∠JPE
∠JPF=∠BPE,
又∠JBP ∠JAC=180°,∠JBP ∠BPE=180°
∠JAC=∠JPF;
J、F、P、A四点共圆;
∠PAF=∠PJF;
又PA为切线∠PAF=∠PBE=∠PJF;
△JFP≌△BEP
PE=PF。
(4)(坎迪定理)如图,设AB是⊙O内一条弦,过AB上一点M任作两弦CD、EF,设CF、ED交AB于P、Q,并设AM=a,BM=b,PM=x,QM=y,则有


坎迪定理
简证:由共角定理得:

(5)M为圆内弦AB的中点,过圆内一点G引两条弦CD和EF,分别交AB于H、K,使得HM=MK,连接CF和ED,分别交AB于P、Q,那么PM=MQ。

M为圆内弦AB的中点,过圆内点G引弦CD和EF,交AB于H、K,使HM=MK,连接CF、ED,交AB于P、Q,那么PM=MQ。
此题证明方法留给读者思考。
(6)如图,H为锐角三角形ABC的垂心,D为BC的中心,过H垂直于DH的直线与边AB,AC分别交于点E,F。求证:HE=HF。

H为锐角三角形ABC的垂心,D为BC的中心,过H垂直于DH的直线与边AB,AC分别交于点E,F。求证:HE=HF
此题证明方法留给读者思考。
4、蝴蝶定理运用
(1)(2002年我爱数学初中生夏令营一试)如图,设AB、CD为⊙O的两直径,过B作PB⊥AB,并与CD延长线相交于点P,过P作直线与⊙O分别交于E、F两点,连结AE,AF分别与CD交于G,H。求证:OG=OH。

2002年我爱数学初中生夏令营一试
(2)(2011新加坡数学奥林匹克)在锐角非等腰Rt△ABC中,AB>AC,O,H分别为△ABC的外心和垂心,Q是AC上的点,且HQ的延长线与BC的延长线交于P,AD⊥BC于D,若BD=DP,求证:∠ODQ=90°。
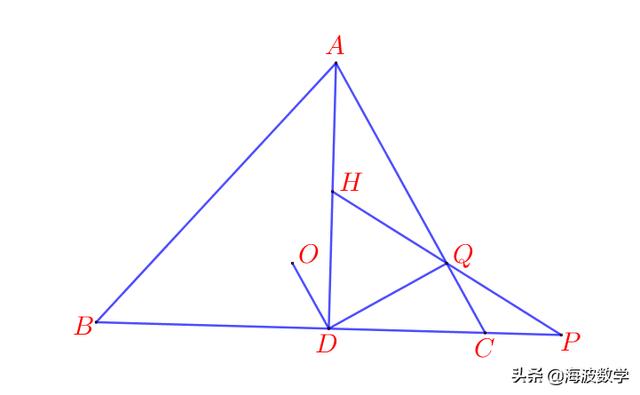
2011新加坡数学奥林匹克
(3)(1990年IMO预选题)已知在锐角三角形ABC中BC>AC,O和H分别是△ABC的外心和垂心,CF是高,过点F且垂直于OF交AC于点P,证明:∠FHP=∠A。

1990年IMO预选题
(4)在锐角三角形ABC中,AM为BC边上的中线,BD⊥AC,CE⊥AB,过点A作AM的垂线交DE延长线于F,FA延长线交BC延长线于G,求证:AF=AG。

(5)如图,△ABC中,AB>AC,BD⊥AC于D,CE⊥AB于E,F为BC中点,AG⊥AF交DE延长线于G,连接GF,求证:AF平分∠GFC。
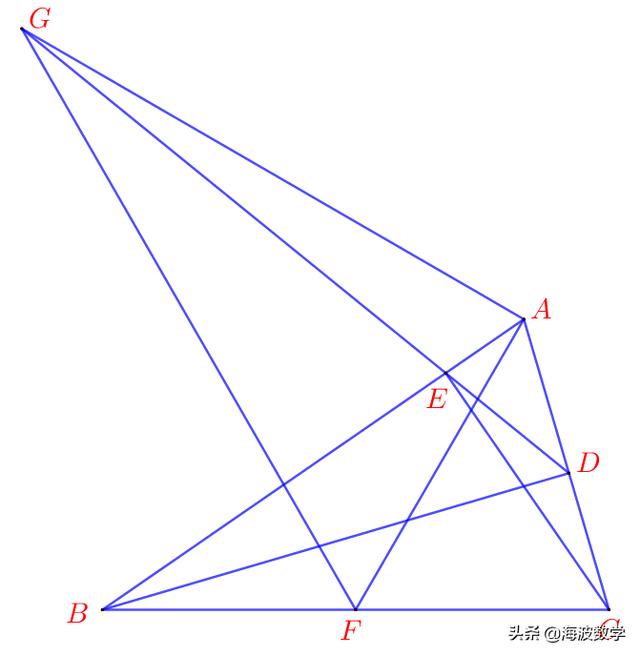
(6)如图,过点A作△ABC外接圆切线,交BC延长线于D,倍长CD至E,作EF//AC交BA延长线于F。求证:OD⊥DF。

(7)如图,已知AD是⊙O的直径,D是BC中点,AB,AC交⊙O于点E,F;EM,FM是⊙O的切线,EM,FM相交于点M,连接DM,求证:DM⊥BC。






