strassen算法（算法入门笔记卡特兰数）

本文来源于力扣圈子，作者：hlxing，力扣（点击查看原文）

一、引言

卡特兰数（Catalan number）是 组合数学 中一个常出现在各种 计数问题 中的 数列。

数列的前几项为：1, 1, 2, 5, 14, 42, 132, 429, 1430, 4862，...

本文将会选取几个经典的卡特兰问题，难度先易后难，带领读者逐个击破解决，最后给出相关的解题模板。

二、经典问题

2.1 进出栈序列

这是一道 最经典 的入门级卡特兰数题目，如果能把这题看懂，相信后面的题目也能迎刃而解。

题目描述

n 个元素进栈序列为：1，2，3，4，...，n，则有多少种出栈序列。

思路

我们将进栈表示为 1，出栈表示为 -1，则 1 3 2 的出栈序列可以表示为： 1 -1 1 1 -1 -1。

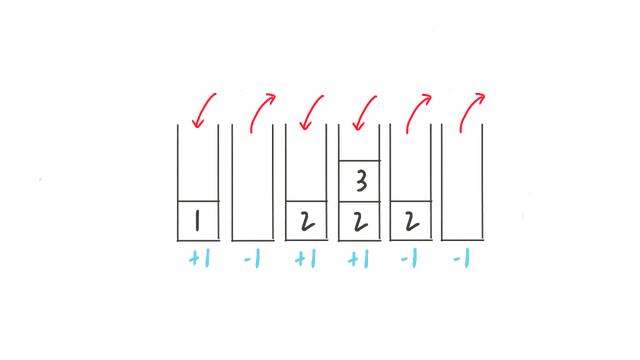
​根据栈本身的特点，每次出栈的时候，必定之前有元素入栈，即对于每个 -1 前面都有一个 1 相对应。因此，出栈序列的 所有前缀和 必然大于等于 0，并且 1 的数量 等于 -1 的数量。

接下来让我们观察一下 n = 3 的一种出栈序列： 1 -1 -1 1 -1 1。序列前三项和小于 0，显然这是个非法的序列。

如果将 第一个 前缀和小于 0 的前缀，即前三项元素都进行取反，就会得到：-1 1 1 1 -1 1。此时有 3 1 个 1 以及 3 - 1 个 -1。

因为这个小于 0 的前缀和必然是 -1，且 -1 比 1 多一个，取反后，-1 比 1 少一个，则 1 变为 n 1 个，且 -1 变为 n - 1 个。进一步推广，对于 n 元素的每种非法出栈序列，都会对应一个含有 n 1 个 1 以及 n - 1个 -1 的序列。

如何证明这两种序列是一一对应的？

假设非法序列为 A，对应的序列为 B。每个 A 只有一个"第一个前缀和小于 0 的前缀"，所以每个 A 只能产生一个 B。而每个 B 想要还原到 A，就需要找到"第一个前缀和大于 0 的前缀"，显然 B 也只能产生一个 A。

每个 B 都有 n 1 个 1 以及 n - 1 个 -1，因此 B 的数量为

相当于在长度为 2n 的序列中找到 n 1 个位置存放 1。相应的，非法序列的数量也就等于

出栈序列的总数量共有

因此，合法的出栈序列的数量为

此时我们就得到了卡特兰数的通项

至于具体如何计算结果将会在后面进行介绍。

2.2 括号序列

题目描述

n 对括号，则有多少种 “括号匹配” 的括号序列

思路

左括号看成 1，右括号看成 -1，那么就和上题的进出栈一样，共有

种序列。

2.3 二叉树

题目描述

n 1 个叶子节点能够构成多少种形状不同的（国际）满二叉树

（国际）满二叉树定义：如果一棵二叉树的结点要么是叶子结点，要么它有两个子结点，这样的树就是满二叉树。

思路

使用深度优先搜索这个满二叉树，向左扩展时标记为 1，向右扩展时标记为 -1。

由于每个非叶子节点都有两个左右子节点，所有它必然会先向左扩展，再向右扩展。总体下来，左右扩展将会形成匹配，即变成进出栈的题型。n 1 个叶子结点会有 2n 次扩展，构成

种形状不同的满二叉树。

2.4 电影购票

题目描述

电影票一张 50 coin，且售票厅没有 coin。m 个人各自持有 50 coin，n 个人各自持有 100 coin。

则有多少种排队方式，可以让每个人都买到电影票。

思路

持有 50 coin 的人每次购票时不需要找零，并且可以帮助后面持有 100 coin 的人找零；而对于持有 100 coin 的人每次购票时需要找零，但 100 coin 对后面的找零没有任何作用。

因此，相当于每个持有 100 coin 的人都需要和一个持有 50 coin 的人进行匹配。我们将持有 50 coin 的标记为 1，持有 100 coin 的标记为 -1，此时又回到了进出栈问题。

不同的是，m 并一定等于 n，且排队序列是一种排列，需要考虑先后顺序，例如各自持有 50 coin 的甲和乙的前后关系会造成两种不同的排队序列。所以，将会有

第二项为什么是

其实很简单，我们每次把第一个前缀小于 0 的前缀取反后，会造成 1 多了一个而 -1 少了一个。这里 1 有 m 个，-1 有 n 个，取反后 1 变成 m 1个，-1 变成 n - 1个，总和不变。

三、解题模板

最后我们需要来计算一下卡特兰数的通项

卡特兰数满足以下递推式：

（证明从略）

因此，我们可以通过递推来得到第 n 个卡特兰数。

代码

Java 实现

Python 实现

需要注意的是，由于卡特兰数增长速度较快，当 n 等于 17 时，卡特兰数将会超过 int 最大值，造成溢出（Python 除外）。对于 Java 语言来说，可以使用 BigInteger 来计算大整数。

那如果 1 的数量不等于 -1 的数量呢，如前面提到的电影购票问题。此时

不是卡特兰数的通项，也就不能够继续使用原有的递推性质。

直接推：

一般而言，为了降低难度，题目会要求我们计算排列数量，所以

四、总结

基本上所有的卡特兰数问题经过一定的转换都可以还原成进出栈问题。因此，只要我们能够学会进出栈问题的解法，无论问题再怎么变化，本质还是不变的。

卡特兰数问题中都会存在一种匹配关系，如进出栈匹配，括号匹配等，一旦计数问题中存在这种关系，那我们就需要去考虑这是否是卡特兰数问题。此外，我们还可以记住序列前四项：1, 1, 2, 5，这些将有利于我们联想到卡特兰数。

目前，力扣已经出现一道卡特兰数问题 力扣 1259. 不相交的握手（点击查看题目），这也是这篇文章编写的原因之一。同时，近年某巴巴，某讯的笔试题中也有出现过这类题目，无非将背景换成买烧饼，借书排队等，相信这些都难不倒读者。

五、扩展

最后留一道比较有意思的卡特兰数问题，欢迎读者留言，提出自己的看法。8 个高矮不同的人需要排成两队，每队 4 个人。其中，每排都是从低到高排列，且第二排的第 i 个人比第一排中第 i 个人高，则有多少种排队方式。

本文作者：hlxing

声明：本文归作者版权所有，如需转载请联系。

,