
离散偏差反应了一组给定数据样本的分散程度。在金融学领域中极为重要。举例来说,如果你要评估一个投资组合的收益风险,比较好的办法是:观察这个投资组合的历史收益率。
如果收益率始终围绕在一个恒定值,假设7%,那么我们会对未来的期望收益率抱有足够的信心,认为该投资组合存在很小的收益风险。而如果收益率没有规律,正负之间变化无常,并且极为分散,那么它的收益风险会使评估者担忧不已。
为了后续演示方便,我们先来用Python生成一组随机样本:

样本集
极差与平均绝对偏差全距(Range),又称极差,定义为数据样本中最大值与最小值的差值,它对数据样本中的异常值是非常敏感的,我们用上面生成的样本集X为例,使用Python包Numpy中的peak to peak方法(ptp)实现如下:

平均绝对偏差(MAD),是“观测值”离“平均值”的平均距离。公式为:

平均绝对偏差公式

方差的定义是:离均差平方和的平均水平,即每一个样本点离开样本均值的距离平方和。用公式表现为:

方差公式
标准差则是方差的平方根。我们同样用Numpy的方差(var)和标准差功能(std)进行计算:

可能有同学看到这里会有疑问:方差和标准差都是衡量样本集的离散程度,那么他们又有什么区别呢?其实区别主要有两点:
第一点是量纲问题,方差由于是平方计算,得出的结果量纲与数据集并不一致。举例来说:你可以说这组同学身高数据标准差的偏差值是10cm,而用方差描述就是偏差值为100c㎡。因此方差容易造成理解上的困难,而标准差不会;第二点是方差的可微分性,方差由于是基于平方的运算,数学上具备可微分性,在一些特定的优化算法上,用方差比标准差或平均绝对偏差更为合适。
可以通过切比雪夫不等式进一步了解标准差。它讲了这么一个事情:任意一个数据集中,位于其平均数m个标准差范围内的比例,总是至少为1-1/㎡(其中m为大于1的任意正数)。
举例来说,对于m=2,m=3和m=5依次有如下结果:所有数据中,至少有3/4的数据位于平均数2个标准差范围内;至少有8/9的数据位于平均数3个标准差范围内;至少有24/25的数据位于平均数5个标准差范围内。我们这里以 m = 1.25 来举例:

切比雪夫不等式的边界似乎相当宽限,但它很有用,因为它适用于所有的数据集和分布。
半方差与半标准差虽然方差和标准差告诉我们数据离“中心”的偏差程度,但它们并不能区分出上偏差还是下偏差。 而一些特殊情况下(如资产回报率),通常我们更关心下偏差。通过半方差和半标准差实现衡量低于均值的观测值的偏差程度。其中,半方差的公式为:

半标准差同样是半方差的平分根。由于Python没有提供内建的函数,我们用自定义函数实现:
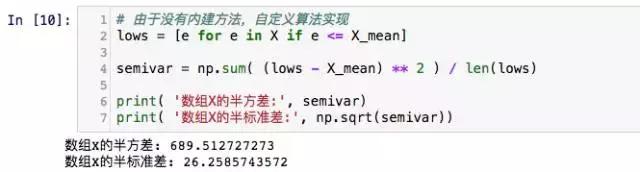
以上就是本期全部内容。本篇为“数据夕拾”量化学堂系列专讲,喜欢请关注吧~
,




